
����Ŀ����ƽ��ֱ������ϵxOy�У���C�İ뾶Ϊr��r��1����P��Բ����Բ��C���غϵĵ㣬��C�������������Ķ������£���ֱ��CP���C���ڵ�A��B������|PA��PB|=2����Ƶ�PΪ��C����������������ͼΪ��C��������������P��ʾ��ͼ��
��1������O�İ뾶Ϊ2ʱ��
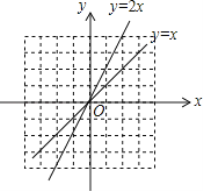
���ڵ�M![]() ��N��0��1����T
��N��0��1����T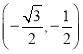 ����O���������������� ����
����O���������������� ����
������O������������P��ֱ��y=![]() x�ϣ���PO�ij�����P�����ꣻ
x�ϣ���PO�ij�����P�����ꣻ
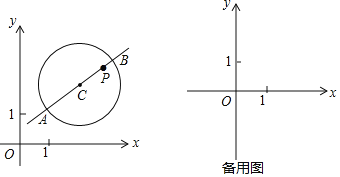
��2����C��Բ����ֱ��y=![]() x+1�ϣ��뾶Ϊ2����y���ϴ��ڡ�C����������������Բ��C��������t��ȡֵ��Χ��
x+1�ϣ��뾶Ϊ2����y���ϴ��ڡ�C����������������Բ��C��������t��ȡֵ��Χ��
���𰸡���1����N��T����PO�ij�Ϊ1����P������Ϊ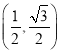 ��
��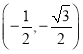 ����2��
����2��![]()
��������
��1��������Բ�ġ������㡱�Ķ���ֱ���жϼ��ɵó����ۣ�
���ȸ���Բ�ġ������㡱�Ķ����г�������⣬�ٽ�P���Ϊ�ڵ�һ���͵�����������������ã�
��2����ȷ��Բ�ġ������㡱�Ĺ켣����ȷ��ȡ��ֵʱ��C��y���λ�ù�ϵ���ã�
�⣺��1���١ߵ�M![]()
�����O��x��Ľ���ΪA��B
�ߡ�O�İ뾶Ϊ2
��ȡA����2��0����B��2��0��
��![]()
���M���ǡ�O�ġ������㡱��ͬ���ɵã���N��T�ǡ�O�ġ������㡱��
�ʴ�Ϊ��N��T��
����ͼ1��
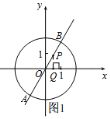
�������⣬![]()
��![]()
��OP=1
����P�ڵ�һ�����ڣ���PQ��x���ڵ�Q
�ߵ�P��ֱ��![]() ��
��
����![]()
��![]() ��
��![]()
��OP=1��![]()
��OQ=![]() ��PQ=
��PQ=![]()
��
����P�ڵ��������ڣ����ݶԳ��Կ�֪������Ϊ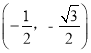
����������PO�ij�Ϊ1����P������Ϊ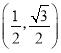 ��
��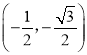 ��
��
��2�����ڡ�C������һ���������㡱P����![]()
��![]()
��CP=1
���������ĵ�P������CP=1������![]() ����
����![]()
�ʶ�������ĵ�P������CP=1ʱ��PΪ��C�ġ������㡱��
��ˣ���C�ġ������㡱�����Ե�CΪԲ�ģ�1Ϊ�뾶��Բ��
��ֱ��![]() ��y�ύ�ڵ�D����ͼ2��
��y�ύ�ڵ�D����ͼ2��
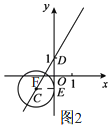
����C�ƶ�����y���������е��ڵ�D���·�ʱ��t��ֵ��С��
���е�ΪE������CE
��![]()
�ߡ�C��Բ����ֱ��![]() ��
��
���ֱ�ߺ�y�ᣬx��Ľ���ֱ���D��0��1����F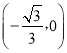
��OF=![]() ��OD=1
��OD=1
��![]()
��CE��OF
��![]()
��![]()
��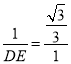
��DE=![]()
��OE=![]()
��t����СֵΪ![]() ��
��
����C�ƶ�����y���������е��ڵ�D���Ϸ�ʱ��t��ֵ���
ͬ���ɵã�t�����ֵΪ![]()
����������t��ȡֵ��ΧΪ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������壩����������һ�����㼰����������Ա��ϵ�����һ�㣬�����ɵ��߶��ܽ������ηָ���������������Σ���������߶�����������ε������ָ��ߣ�
�����ԣ�
��1����ͼ���� Rt��ABC �У���C��90������A��30��������ֱ�ߺ�Բ�滭����ABC �������ָ��ߣ�
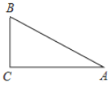
��2����һ��ֱ�������������������ָ��ߣ���������ֱ����������С�ڽǵĶ�����
��̽����
��3��һ�����������ε�����Ϊ 8������һ�������ָ��߷ֵõ���������������һ����������ԭ���������ƣ����Ӧ�����ָ��ߵij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ���
��ֱ���![]() ���㣬����
���㣬����![]() ���߶�
���߶�![]() ���ƶ�����
���ƶ�����![]() ���غϣ�����
���غϣ�����![]() Ϊ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
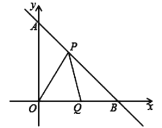
��1�����![]() �͵�
�͵�![]() �����ꣻ
�����ꣻ
��2����֤��![]() ��
��
��3���Ƿ���ڵ�![]() ʹ��
ʹ��![]() �ǵ��������Σ������ڣ���ֱ��д����
�ǵ��������Σ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺����ѧϰ��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬������ͼ1����![]() �У�
��![]() ������
������![]() ���
��б��![]() ���е㣬��
���е㣬��![]()
���Ӧ�ã���ͼ2��![]() �У�
��![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() ���۵õ�
���۵õ�![]() ����
����![]() ��
��
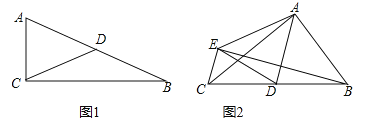
��1���߶�![]() �ij��� ��
�ij��� ��
��2���ж�![]() ����״��˵�����ɣ�
����״��˵�����ɣ�
��3���߶�![]() �ij��� ��
�ij��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����m�������1��������Щ�����ɫ�����������
��1����ÿ�ν����ֽ��Ⱥ���������1���������ɫ�ٷŻغ��ӣ�ͨ�������ظ�����������������Ƶ���ȶ���0.75���ң���m��ֵӦ���� ����
��2���ڣ�1���������£���m�������1���������������Ϸ���ȴӺ��������ȡһ�����ٴ�ʣ�µ������������ȡһ�������¼����������������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �Ķ���
�Ķ���![]() ��
��![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����P��Q���㣬
����P��Q���㣬![]() .
.
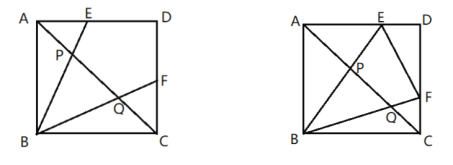
��1����![]() ʱ��
ʱ��
����![]() �Ķ�����
�Ķ�����
������![]() Ϊ�߳��������������
Ϊ�߳��������������
��2����![]() ��
��![]() ���˶�ʱ��ʼ�ձ���
���˶�ʱ��ʼ�ձ���![]() ������
������![]() ����
����![]() �������СֵΪ ��ֱ��д���𰸣���
�������СֵΪ ��ֱ��д���𰸣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������![]() ��x��0����ͼ����A��2����1����B��
��x��0����ͼ����A��2����1����B��![]() ��n�����㣬ֱ��y=2��y�ύ�ڵ�C��
��n�����㣬ֱ��y=2��y�ύ�ڵ�C��

��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�M��N�ֱ�������CB������DC�ϵĶ��㣬��ʼ�ա�MAN��45����

��1����ͼ1������M��N�ֱ����߶�BC��DC��ʱ����ֱ��д���߶�BM��MN��DN֮���������ϵ��
��2����ͼ2������M��N�ֱ���CB��DC���ӳ�����ʱ����1���еĽ����Ƿ���Ȼ������������������֤��������������д����ȷ�Ľ��ۣ���֤����
��3����ͼ3������M��N�ֱ���CB��DC���ӳ�����ʱ����CN��CD��6����BD��AM���ӳ��߽��ڵ�P����AN��Q��ֱ��д��AQ��AP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪��![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() �㣬��
�㣬��![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ���������Բ
���������Բ![]() ��
��![]() ��
��![]() ����
����![]() ��
��
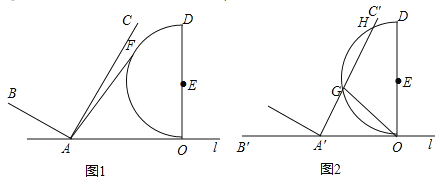
��1������Բ![]() ����һ��
����һ��![]() ����
����![]() �����ֵΪ__________����СֵΪ__________��
�����ֵΪ__________����СֵΪ__________��
��2��������ֱ��![]() ƽ��
ƽ��![]() �õ�
�õ�![]() ��
��
����ͼ2����![]() �ذ�Բ
�ذ�Բ![]() �Ļ�
�Ļ�![]() �ij�Ϊ
�ij�Ϊ![]() ����
����![]() �Ķ�����
�Ķ�����
�ڵ���Բ![]() ��
��![]() �ı�����ʱ����ƽ�ƾ��룮
�ı�����ʱ����ƽ�ƾ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com