
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФКажагаmИіКкЧђКЭ1ИіАзЧђЃЌетаЉЧђГ§беЩЋЭтЮоЦфЫћВюБ№ЃЎ
ЃЈ1ЃЉШєУПДЮНЋЧђГфЗжНСдШКѓЃЌШЮвтУўГі1ИіЧђМЧЯТбеЩЋдйЗХЛиКазгЃЎЭЈЙ§ДѓСПжиИДЪдбщКѓЃЌЗЂЯжУўЕНКкЧђЕФЦЕТЪЮШЖЈдк0.75зѓгвЃЌдђmЕФжЕгІЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌгУmИіКкЧђКЭ1ИіАзЧђНјааУўЧђгЮЯЗЃЎЯШДгКажаЫцЛњУўШЁвЛИіЧђЃЌдйДгЪЃЯТЕФЧђжадйЫцЛњУўШЁвЛИіЧђЃЌЧѓЪТМўЁАЯШУўЕНКкЧђЃЌдйУўЕНАзЧђЁБЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3ЃЛЃЈ2ЃЉМћНтЮіЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§ДѓСПжиИДЪдбщЗЂЯжУўЕНЕФКкЧђЕФЦЕТЪЮШЖЈдк0.75зѓгвЃЌПЩЕУКкЧђеМаЁЧђзмЪ§ЕФ0.75МДПЩЧѓГіД№АИ
ЃЈ2ЃЉЛГіЪїзДЭМЃЌДгЪїзДЭМПЩжЊЃЌЁАЯШДгКажаЫцЛњУўШЁвЛИіЧђЃЌдйДгЪЃЯТЕФЧђжадйЫцЛњУўШЁвЛИіЧђЁБЙВга12жжЕШПЩФмЕФНсЙћЃЌЦфжаЁАЯШУўЕНКкЧђЃЌдйУўЕНАзЧђЁБЕФНсЙћга3жжМДПЩЧѓГіД№АИ
НтЃКЃЈ1ЃЉЙ§ДѓСПжиИДЪдбщЗЂЯжУўЕНЕФКкЧђЕФЦЕТЪЮШЖЈдк0.75зѓгвЃЌПЩЕУКкЧђеМаЁЧђзмЪ§ЕФ0.75ЃЌЙЪ![]() ЃЌНтЕУm=3ЃЛЙЪmЕФжЕгІЪЧ3
ЃЌНтЕУm=3ЃЛЙЪmЕФжЕгІЪЧ3
ЃЈ2ЃЉЛГіЪїзДЭМШчЯТЃЈСаБэЗЈВЮееИјЗжЃЉЃЛ

ДгЪїзДЭМПЩжЊЃЌЁАЯШДгКажаЫцЛњУўШЁвЛИіЧђЃЌдйДгЪЃЯТЕФЧђжадйЫцЛњУўШЁвЛИіЧђЁБЙВга12жжЕШПЩФмЕФНсЙћЃЌЦфжаЁАЯШУўЕНКкЧђЃЌдйУўЕНАзЧђЁБЕФНсЙћга3жжЃЛ
ЁрPЃЈЯШУўЕНКкЧђЃЌдйУўЕНАзЧђЃЉ=![]() =
=![]()


 ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
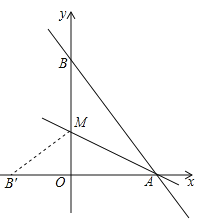
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛДЮКЏЪ§y=kx+bгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЈ2ЃЌ4ЃЉЃЌBЃЈЉ4ЃЌnЃЉСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈ2ЃЌ4ЃЉЃЌBЃЈЉ4ЃЌnЃЉСНЕуЃЎ
ЃЈ1ЃЉЗжБ№ЧѓГівЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊЕуCЃЌСЌНгACЃЌЧѓЁїACBЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
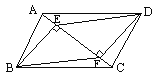
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌ![]() ABCDжаЃЌEЁЂFЗжБ№ЪЧACЩЯСНЕуЃЌЧвBEЁЭACгкEЃЌDFЁЭACгкFЃЎЧѓжЄЃКЫФБпаЮBEDFЪЧЦНааЫФБпаЮЃЎ
ABCDжаЃЌEЁЂFЗжБ№ЪЧACЩЯСНЕуЃЌЧвBEЁЭACгкEЃЌDFЁЭACгкFЃЎЧѓжЄЃКЫФБпаЮBEDFЪЧЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() КЭЕу
КЭЕу![]() ЪЧ
ЪЧ![]() ЩЯЕФвЛЕуЃЌШєНЋ
ЩЯЕФвЛЕуЃЌШєНЋ![]() би
би![]() елЕўЃЌЕу
елЕўЃЌЕу![]() ЧЁКУТфдк
ЧЁКУТфдк![]() жсЩЯЕФЕу
жсЩЯЕФЕу![]() ДІЃЌдђЕу
ДІЃЌдђЕу![]() ЕФзјБъЮЊ______ЃЎ
ЕФзјБъЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНx2Љ4x+nЃЈxЃО0ЃЉЕФЭМЯѓМЧЮЊG1ЃЌНЋG1ШЦзјБъдЕуа§зЊ180ЁуЕУЕНЭМЯѓG2ЃЌЭМЯѓG1КЭG2КЯЦ№РДМЧЮЊЭМЯѓGЃЎ
ЃЈ1ЃЉШєЕуPЃЈЉ1ЃЌ2ЃЉдкЭМЯѓGЩЯЃЌЧѓnЕФжЕЃЎ
ЃЈ2ЃЉЕБnЃНЉ1ЪБЃЎ
ЂйШєQЃЈtЃЌ1ЃЉдкЭМЯѓGЩЯЃЌЧѓtЕФжЕЃЎ
ЂкЕБkЁмxЁм3ЃЈkЃМ3ЃЉЪБЃЌЭМЯѓGЖдгІКЏЪ§ЕФзюДѓжЕЮЊ5ЃЌзюаЁжЕЮЊЉ5ЃЌжБНгаДГіkЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉЕБвдAЃЈЉ3ЃЌ3ЃЉЁЂBЃЈЉ3ЃЌЉ1ЃЉЁЂCЃЈ2ЃЌЉ1ЃЉЁЂDЃЈ2ЃЌ3ЃЉЮЊЖЅЕуЕФОиаЮABCDЕФБпгыЭМЯѓGгаЧвжЛгаШ§ИіЙЋЙВЕуЪБЃЌжБНгаДГіnЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
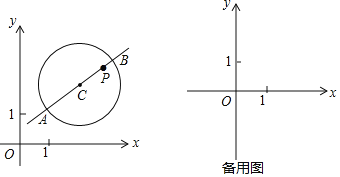
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЁбCЕФАыОЖЮЊrЃЈrЃО1ЃЉЃЌPЪЧдВФкгыдВаФCВЛжиКЯЕФЕуЃЌЁбCЕФЁАЭъУРЕуЁБЕФЖЈвхШчЯТЃКШєжБЯпCPгыЁбCНЛгкЕуAЃЌBЃЌТњзу|PAЉPB|=2ЃЌдђГЦЕуPЮЊЁбCЕФЁАЭъУРЕуЁБЃЌШчЭМЮЊЁбCМАЦфЁАЭъУРЕуЁБPЕФЪОвтЭМЃЎ
ЃЈ1ЃЉЕБЁбOЕФАыОЖЮЊ2ЪБЃЌ
ЂйдкЕуM![]() ЃЌNЃЈ0ЃЌ1ЃЉЃЌT
ЃЌNЃЈ0ЃЌ1ЃЉЃЌT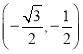 жаЃЌЁбOЕФЁАЭъУРЕуЁБЪЧЁЁ ЁЁЃЛ
жаЃЌЁбOЕФЁАЭъУРЕуЁБЪЧЁЁ ЁЁЃЛ
ЂкШєЁбOЕФЁАЭъУРЕуЁБPдкжБЯпy=![]() xЩЯЃЌЧѓPOЕФГЄМАЕуPЕФзјБъЃЛ
xЩЯЃЌЧѓPOЕФГЄМАЕуPЕФзјБъЃЛ
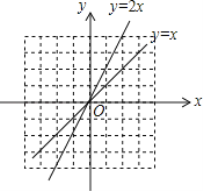
ЃЈ2ЃЉЁбCЕФдВаФдкжБЯпy=![]() x+1ЩЯЃЌАыОЖЮЊ2ЃЌШєyжсЩЯДцдкЁбCЕФЁАЭъУРЕуЁБЃЌЧѓдВаФCЕФзнзјБъtЕФШЁжЕЗЖЮЇЃЎ
x+1ЩЯЃЌАыОЖЮЊ2ЃЌШєyжсЩЯДцдкЁбCЕФЁАЭъУРЕуЁБЃЌЧѓдВаФCЕФзнзјБъtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
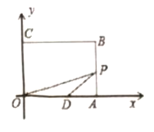
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЗжБ№дкзјБъжсЩЯЃЌ
ЗжБ№дкзјБъжсЩЯЃЌ![]() ЃЌЕу
ЃЌЕу![]() би
би![]() дЫЖЏЃЌСЌНг
дЫЖЏЃЌСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊЕШбќШ§НЧаЮЪБЃЌЕу
ЮЊЕШбќШ§НЧаЮЪБЃЌЕу![]() ЕФзјБъЮЊ__________ЃЎ
ЕФзјБъЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЈ-6ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЕуCдкжБЯп![]() ЩЯЃЌдђЪЙЁїABCЪЧжБНЧШ§НЧаЮЕФЕуCЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
ЩЯЃЌдђЪЙЁїABCЪЧжБНЧШ§НЧаЮЕФЕуCЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
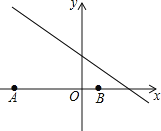
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃК![]() жаЃЌ
жаЃЌ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЌЯТУцаДГіПЩдЫгУЗДжЄЗЈжЄУїетИіУќЬтЕФЫФИіВНжшЃК
ЃЌЯТУцаДГіПЩдЫгУЗДжЄЗЈжЄУїетИіУќЬтЕФЫФИіВНжшЃК
ЂйЁр![]() ЃЌетгыШ§НЧаЮФкНЧКЭЮЊ
ЃЌетгыШ§НЧаЮФкНЧКЭЮЊ![]() УЌЖм,ЂквђДЫМйЩшВЛГЩСЂЃЎЁр
УЌЖм,ЂквђДЫМйЩшВЛГЩСЂЃЎЁр![]() ,ЂлМйЩшдк
,ЂлМйЩшдк![]() жаЃЌ
жаЃЌ![]() ,ЂмгЩ
,ЂмгЩ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌМД
ЃЌМД![]() ЃЎетЫФИіВНжше§ШЗЕФЫГађгІЪЧЃЈЁЁЁЁЃЉ
ЃЎетЫФИіВНжше§ШЗЕФЫГађгІЪЧЃЈЁЁЁЁЃЉ
A.ЂлЂмЂкЂйB.ЂлЂмЂйЂкC.ЂйЂкЂлЂмD.ЂмЂлЂйЂк
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com