
如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连结BE交AC于F,连结FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD②△FED与△DEB③△CFD与△ABG④△ADF与△CFB中相似的为( )
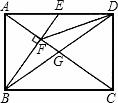
A.①④ B.①② C.②③④ D.①②③
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为( ).
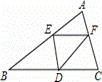

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为( ).
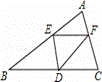

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.线段DC上有一点E,当△ABE的面积等于5时,点E的坐标为 .
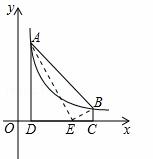
查看答案和解析>>
科目:初中数学 来源: 题型:
某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

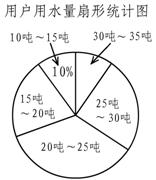
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com