
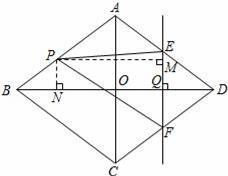
如图,在菱形ABCD中,AC、BD交于点O,AC=12cm,BD=16cm.动点P在线段AB上,由B向A运动,速度为1cm/s,动点Q在线段OD上,由D向O运动,速度为1cm/s.过点Q作直线EF⊥BD交AD于E,交CD于F,连接PF,设运动时间为t(0<t<8).问:
(1)何时四边形APFD为平行四边形?求出相应t的值;
(2)设四边形APFE面积为ycm2,求y与t的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出相应t的值,并求出,P、E两点间的距离;若不存在,说明理由.


【考点】四边形综合题.
【专题】几何动点问题.
【分析】(1))由四边形ABCD是菱形,OA=
 AC,OB=
AC,OB=
 BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出
BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出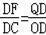
 .求出DF.由AP=DF.求出t.
.求出DF.由AP=DF.求出t.
(2)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG=
 AC•BD,求出CG.据S梯形APFD=
AC•BD,求出CG.据S梯形APFD=
 (AP+DF)•CG.S△EFD=
(AP+DF)•CG.S△EFD=
 EF•QD.得出y与t之间的函数关系式;
EF•QD.得出y与t之间的函数关系式;
(3)过点C作CG⊥AB于点G,由S菱形ABCD=AB•CG,求出CG,由S四边形APFE:S菱形ABCD=17:40,求出t,再由△PBN∽△ABO,求得PN,BN,据线段关系求出EM,PM再由勾股定理求出PE.
【解答】解:(1)∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,OA=OC=
 AC=6,OB=OD=
AC=6,OB=OD=
 BD=8.
BD=8.
在Rt△AOB中,AB=
 =10.
=10.
∵EF⊥BD,
∴∠FQD=∠COD=90°.
又∵∠FDQ=∠CDO,
∴△DFQ∽△DCO.
∴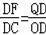
 .
.
即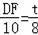
 ,
,
∴DF=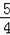
 t.
t.
∵四边形APFD是平行四边形,
∴AP=DF.
即10﹣t=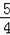
 t,
t,
解这个方程,得t=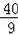
 .
.
∴当t=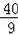
 s时,四边形APFD是平行四边形.
s时,四边形APFD是平行四边形.
(2)如图,过点C作CG⊥AB于点G,
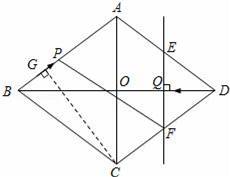

∵S菱形ABCD=AB•CG=
 AC•BD,
AC•BD,
即10•CG=
 ×12×16,
×12×16,
∴CG=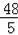
 .
.
∴S梯形APFD=
 (AP+DF)•CG
(AP+DF)•CG
=
 (10﹣t+
(10﹣t+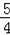
 t)•
t)•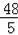
 =
=
 t+48.
t+48.
∵△DFQ∽△DCO,
∴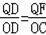
 .
.
即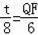
 =,
=,
∴QF=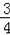
 t.
t.
同理,EQ=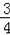
 t.
t.
∴EF=QF+EQ=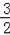
 t.
t.
∴S△EFD=
 EF•QD=
EF•QD=
 ×
×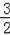
 t×t=
t×t=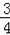
 t2.
t2.
∴y=(
 t+48)﹣
t+48)﹣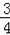
 t2=﹣
t2=﹣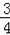
 t2+
t2+
 t+48.
t+48.
(3)如图,过点P作PM⊥EF于点M,PN⊥BD于点N,

若S四边形APFE:S菱形ABCD=17:40,
则﹣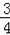
 t2+
t2+
 t+48=
t+48=
 ×96,
×96,
即5t2﹣8t﹣48=0,
解这个方程,得t1=4,t2=﹣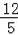
 (舍去)
(舍去)
过点P作PM⊥EF于点M,PN⊥BD于点N,
当t=4时,
∵△PBN∽△ABO,
∴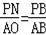
 =
=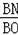
 ,
,
即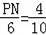
 =
=
 .
.
∴PN=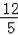
 ,BN=
,BN=
 .
.
∴EM=EQ﹣MQ=3﹣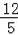
 =
=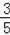
 .
.
PM=BD﹣BN﹣DQ=16﹣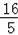
 ﹣4=
﹣4=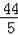
 .
.
在Rt△PME中,
PE=
 =
=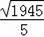
 (cm).
(cm).
【点评】本题主要考查了四边形的综合知识,用到的知识点有勾股定理、菱形的性质、梯形的面积公式、相似三角形的判定和性质以及一元二次方程得解、平行四边形的性质等性质,题目的综合性较强,对学生的综合解题能力要求很高,是一道不错的中考压轴题.


科目:初中数学 来源: 题型:
我市股市交易中心每买、卖一次需千分之七点五的各种费用,某投资者以每股10元的价格买入上海某股票1000股,当该股票涨到12元时全部卖出,该投资者实际盈利为( )
A.2000元 B.1925元 C.1835元 D.1910元
查看答案和解析>>
科目:初中数学 来源: 题型:
两位同学在解方程组时,甲同学由 正确地解出
正确地解出 ,乙同学因把C写错了解得
,乙同学因把C写错了解得  ,那么a、b、c的正确的值应为( )
,那么a、b、c的正确的值应为( )
A、a=4,b=5,c=-1 B、a=4,b=5,c=-2
C、a=-4,b=-5,c=0 D、a=-4,b=-5,c=2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在3×3的方格内,填写了一些代数式和数
(1)在图中各行、各列及对角线上三个数之和都相等,请你求出x,y的值。
(2)把满足(1)的其它6个数填入图(2)中的方格内。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,E是BC中点,点O在AB上,以OB为半径的⊙O经过点AE上的一点M,分别交AB,BC于点F,G,连BM,此时∠FBM=∠CBM.
(1)求证:AM是⊙O的切线;
(2)当BC=6,OB:OA=1:2 时,求
 ,AM,AF围成的阴影部分面积.
,AM,AF围成的阴影部分面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
已知,如图,双曲线y=
 (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=
 (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
(1)AB与CD的位置关系是 ;
(2)四边形ABDC的面积为 .


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com