
如图,在△ABC中,AB=AC,E是BC中点,点O在AB上,以OB为半径的⊙O经过点AE上的一点M,分别交AB,BC于点F,G,连BM,此时∠FBM=∠CBM.
(1)求证:AM是⊙O的切线;
(2)当BC=6,OB:OA=1:2 时,求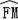
 ,AM,AF围成的阴影部分面积.
,AM,AF围成的阴影部分面积.


【考点】切线的判定;勾股定理;扇形面积的计算;相似三角形的判定与性质.
【专题】计算题.
【分析】(1)连接OM,由AB=AC,且E为BC中点,利用三线合一得到AE垂直于BC,再由OB=OM,利用等边对等角得到一对角相等,由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OM与BC平行,可得出OM垂直于AE,即可得证;
(2)由E为BC中点,求出BE的长,再由OB与OA的比值,以及OB=OM,得到OM与OA的比值,由OM垂直于AE,利用直角三角形中一直角边等于斜边的一半,得到此直角边所对的角为30度得到∠MAB=30°,∠MOA=60°,阴影部分的面积=三角形AOM面积﹣扇形MOF面积,求出即可.
【解答】解:(1)连结OM,
∵AB=AC,E是BC中点,
∴BC⊥AE,
∵OB=OM,
∴∠OMB=∠MBO,
∵∠FBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC,
∴OM⊥AE,
∴AM是⊙O的切线;
(2)∵E是BC中点,
∴BE=
 BC=3,
BC=3,
∵OB:OA=1:2,OB=OM,
∴OM:OA=1:2,
∵OM⊥AE,
∴∠MAB=30°,∠MOA=60°,OA:BA=1:3,
∵OM∥BC,
∴△AOM∽△ABE,
∴
 =
=
 =
=
 ,
,
∴OM=2,
∴AM=
 =2
=2
 ,
,
∴S阴影=
 ×2
×2
 ×2﹣
×2﹣
 =2
=2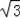
 ﹣
﹣
 π.
π.


【点评】此题考查了切线的判定,涉及的知识有:圆周角定理,弧,弦及圆心角之间的关系,平行线的性质,扇形面积求法,以及勾股定理,熟练掌握切线的判定方法是解本题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是( )
A.2小时 B.2.2小时 C.2.25小时 D.2.4小时

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在菱形ABCD中,AC、BD交于点O,AC=12cm,BD=16cm.动点P在线段AB上,由B向A运动,速度为1cm/s,动点Q在线段OD上,由D向O运动,速度为1cm/s.过点Q作直线EF⊥BD交AD于E,交CD于F,连接PF,设运动时间为t(0<t<8).问:
(1)何时四边形APFD为平行四边形?求出相应t的值;
(2)设四边形APFE面积为ycm2,求y与t的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出相应t的值,并求出,P、E两点间的距离;若不存在,说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com