
如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标;
(3)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,直接写出点P的坐标;若不存在,请说明理由.

(1)抛物线为y=-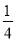 x2+
x2+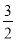 x+4.(2)M的坐标为(6,4)或(3-
x+4.(2)M的坐标为(6,4)或(3- ,-4)或(3+
,-4)或(3+ ,-4).(3)点P的坐标为(4+
,-4).(3)点P的坐标为(4+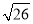 ,
,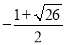 )或(4-
)或(4-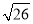 ,
,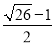 )或(-1+
)或(-1+ ,-8+2
,-8+2 )或(-1-
)或(-1- ,-8-2
,-8-2 ).
).
【解析】
试题分析:(1)解析式已存在,y=ax2+bx+4,我们只需要根据特点描述求出a,b即可.由对称轴为-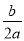 ,又过点A(-2,0),所以函数表达式易得.
,又过点A(-2,0),所以函数表达式易得.
(2)四边形为平行四边形,则必定对边平行且相等.因为已知MN∥BC,所以MN=BC,即M、N的位置如B、C位置关系,则可分2种情形,①N点在M点右下方,即M向下平行4个单位,向右2个单位与N重合;②M点在N右下方,即N向下平行4个单位,向右2个单位与M重合.因为M在抛物线,可设坐标为(x,-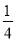 x2+
x2+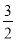 x+4),易得N坐标.由N在x轴上,所以其纵坐标为0,则可得关于x的方程,进而求出x,求出M的坐标.
x+4),易得N坐标.由N在x轴上,所以其纵坐标为0,则可得关于x的方程,进而求出x,求出M的坐标.
(3)使△PBD≌△PBC,易考虑∠CBD的平分线与抛物线的交点.确定平分线可因为BC=BD,可作等腰△BCD,利用三线合一,求其中线所在方程,进而与抛物线联立得方程组,解出P即可.
试题解析:(1)∵抛物线y=ax2+bx+4交x轴于A(-2,0),
∴0=4a-2b+4,
∵对称轴是x=3,
∴-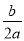 =3,即6a+b=0,
=3,即6a+b=0,
两关于a、b的方程联立解得 a=-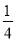 ,b=
,b=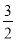 ,
,
∴抛物线为y=-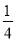 x2+
x2+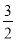 x+4.
x+4.
(2)∵四边形为平行四边形,且BC∥MN,
∴BC=MN.
①N点在M点右下方,即M向下平移4个单位,向右平移2个单位与N重合.
设M(x,-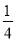 x2+
x2+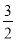 x+4),则N(x+2,-
x+4),则N(x+2,-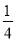 x2+
x2+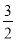 x),
x),
∵N在x轴上,
∴-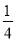 x2+
x2+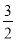 x=0,
x=0,
解得 x=0(M与C重合,舍去),或x=6,
∴xM=6,
∴M(6,4).
②M点在N右下方,即N向下平行4个单位,向右2个单位与M重合.
设M(x,- 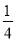 x2+
x2+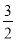 x+4),则N(x-2,-
x+4),则N(x-2,-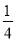 x2+
x2+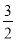 x+8),
x+8),
∵N在x轴上,
∴-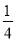 x2+
x2+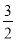 x+8=0,
x+8=0,
解得 x=3- ,或x=3+
,或x=3+ ,
,
∴xM=3- ,或3+
,或3+ .
.
∴M(3- ,-4)或(3+
,-4)或(3+ ,-4)
,-4)
综上所述,M的坐标为(6,4)或(3- ,-4)或(3+
,-4)或(3+ ,-4).
,-4).
(3)∵OC=4,OB=3,
∴BC=5.
如果△PBD≌△PBC,那么BD=BC=5,
∵D在x轴上,
∴D为(-2,0)或(8,0).
①当D为(-2,0)时,连接CD,过B作直线BE平分∠DBC交CD于E,交抛物线于P1,P2,
此时△P1BC≌△P1BD,△P2BC≌△P2BD,
∵BC=BD,
∴E为CD的中点,即E(-1,2),
设过E(-1,2),B(3,0)的直线为y=kx+b,则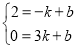 ,
,
解得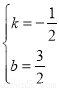 ,
,
∴BE:y=-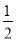 x+
x+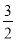 .
.
设P(x,y),则有 ,
,
解得  ,或
,或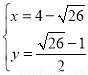 ,
,
则P1(4+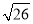 ,
,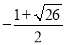 ),P2(4-
),P2(4-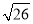 ,
,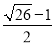 ).
).
②当D为(8,0)时,连接CD,过B作直线BF平分∠DBC交CD于F,交抛物线于P3,P4,
此时△P3BC≌△P3BD,△P4BC≌△P4BD,
∵BC=BD,
∴F为CD的中点,即E(4,2),
设过E(4,2),B(3,0)的直线为y=kx+b,则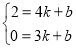 ,
,
解得  ,
,
∴BF:y=2x-6.
设P(x,y),则有 ,
,
解得  或
或  ,
,
则P3(-1+ ,-8+2
,-8+2 ),P4(-1-
),P4(-1- ,-8-2
,-8-2 ).
).
综上所述,点P的坐标为(4+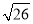 ,
,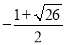 )或(4-
)或(4-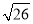 ,
,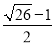 )或(-1+
)或(-1+ ,-8+2
,-8+2 )或(-1-
)或(-1- ,-8-2
,-8-2 ).
).
【考点】二次函数综合题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:2014年初中毕业升学考试(福建南平卷)数学(解析版) 题型:填空题
将直尺和三角板按如图的样子叠放在一起,则∠1+∠2的度数是( )

A.45° B.60° C.90° D.180°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:解答题
如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.7米范围内,问小明种植的这两棵树是否符合这个要求?
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:填空题
如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是 (写出一个即可).

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃天水卷)数学(解析版) 题型:解答题
如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连结DB交EF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:选择题
若反比例函数 的图象位于第二、四象限,则k的取值可以是( )
的图象位于第二、四象限,则k的取值可以是( )
A.0 B.1 C.2 D.以上都不是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com