
分析 利用平均数求法和方差的方法分别列式求得平均数和方差得出答案即可.
解答 解:∵x1、x2、…xn的平均数为2,
∴x1+x2+…+xn=2n,
∴$\frac{2{x}_{1}+5+2{x}_{2}+5+…+2{x}_{n}+5}{n}$=2×2+5=9,
∵原平均数为2,新数据的平均数变为9,
则原来的方差S12=$\frac{1}{n}$[(x1-2)2+(x2-2)2+…+(xn-2)2]=3,
现在的方差S22=$\frac{1}{n}$[(2x1+5-9)2+(2x2+5-9)2+…+(2xn+5-9)2]
=$\frac{1}{n}$[4(x1-2)2+4(x2-2)2+…+4(xn-2)2]=4×3=12.
故答案为:9,12.
点评 此题考查平均数与方差的意义,掌握平均数与方差的计算方法是解决问题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.
如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系xOy中,直线l过点(0,1)且与x轴平行,△ABC关于直线l对称,已知点A坐标是(4,4),则点B的坐标是(4,-2).
如图,在直角坐标系xOy中,直线l过点(0,1)且与x轴平行,△ABC关于直线l对称,已知点A坐标是(4,4),则点B的坐标是(4,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知平行四边形ABCD.
如图,已知平行四边形ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
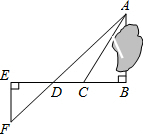 了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:
了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com