
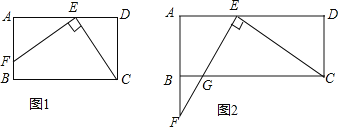
【题目】在矩形ABCD中,已知AD>AB.在边AD上取点E,使AE=AB,连结CE,过点E作EF⊥CE,与边AB或其延长线交于点F.
(1)如图1,当点F在边AB上时,线段AF与DE的大小关系为 .
(2)如图2,当点F在边AB的延长线上时,EF与边BC交于点G.判断线段AF与DE的大小关系,并加以证明.
(3)如图2,若AB=2,AD=5,求线段BG的长.
【答案】(1)AF=DE;(2)AF=DE;证明见解析;(3)![]()
【解析】
1)根据题意证明△AEF≌△DCE即可解答;
(2)证明方法与(1)相同可以证明结论;
(3)根据平行线分线段成比例定理列出比例式,计算得到答案.
(1)AF=DE;
理由是:如图1,∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=CD,
∵AE=AB,
∴AE=CD,
∵EF⊥CE,
∴∠FEC=∠AEF+∠CED=∠CED+∠ECD=90°,
∴∠AEF=∠ECD,
在△AEF和△DCE中,
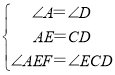 ,
,
∴△AEF≌△DCE(ASA),
∴AF=DE;
故答案为:AF=DE;
(2)AF=DE,
证明:如图2,∵∠A=∠FEC=∠D=90°,
∴∠AEF=∠DCE,
在△AEF和△DCE中,
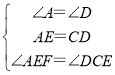 ,
,
∴△AEF≌△DCE(ASA),
∴AF=DE.
(3)∵△AEF≌△DCE,
∴AE=CD=AB=2,AF=DE=3,FB=FA﹣AB=1,
∵BG∥AD,
∴![]() ,即
,即![]()
∴BG=![]() .
.


科目:初中数学 来源: 题型:
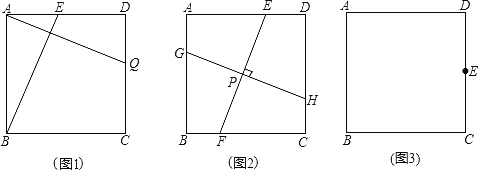
【题目】在习题课上,老师让同学们以课本一道习题“如图1,A,B,C,D四家工厂分别坐落在正方形城镇的四个角上.仓库E和Q分别位于AD和DC上,且ED=QC.证明两条直路BE=AQ且BE⊥AQ.”为背景开展数学探究.
(1)独立思考:将上题条件中的ED=QC去掉,将结论中的BE⊥AQ变为条件,其他条件不变,那么BE=AQ还成立吗?请写出答案并说明理由;
(2)合作交流:“祖冲之”小组的同学受此问题的启发提出:如图2,在正方形ABCD内有一点P,过点P作EF⊥GH,点E、F分别在正方形的对边AD、BC上,点G、H分别在正方形的对边AB、CD上,那么EF与GH相等吗?并说明理由.
(3)拓展应用:“杨辉”小组的同学受“祖冲之”小组的启发,想到了利用图2的结论解决以下问题:
如图3,将边长为10cm的正方形纸片ABCD折叠,使点A落在DC的中点E处,折痕为MN,点N在BC边上,点M在AD边上.请你画出折痕,则折痕MN的长是 ;线段DM的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
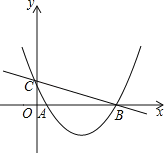
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 和点
和点![]() .
.
(1)求抛物线的解析式;
(2)求直线![]() 的解析式;
的解析式;
(3)若点![]() 是抛物线上的动点,过点
是抛物线上的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,以
,以![]() ,
,![]() ,
,![]() 为顶点的三角形是否能够与
为顶点的三角形是否能够与![]() 相似(排除全等的情况)?若能,请求出所有符合条件的点
相似(排除全等的情况)?若能,请求出所有符合条件的点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑销售商试销某一品牌电脑(出厂为![]() 元/台)以
元/台)以![]() 元/台销售时,平均每月可销售
元/台销售时,平均每月可销售![]() 台,现为了扩大销售,销售商决定降价销售,在原来
台,现为了扩大销售,销售商决定降价销售,在原来![]() 月份平均销售量的基础上,经
月份平均销售量的基础上,经![]() 月份的市场调查,
月份的市场调查,![]() 月份调整价格后,月销售额达到
月份调整价格后,月销售额达到![]() 元.已知电脑价格每台下降
元.已知电脑价格每台下降![]() 元,月销售量将上升
元,月销售量将上升![]() 台.
台.
![]() 求
求![]() 月份到
月份到![]() 月份销售额的月平均增长率;
月份销售额的月平均增长率;
![]() 求
求![]() 月份时该电脑的销售价格.
月份时该电脑的销售价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
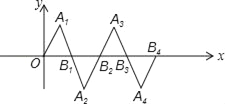
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东台市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知![]() 年投资
年投资![]() 万元,预计
万元,预计![]() 年投资
年投资![]() 万元.若这两年内平均每年投资增长的百分率相同.
万元.若这两年内平均每年投资增长的百分率相同.
![]() 求平均每年投资增长的百分率;
求平均每年投资增长的百分率;
![]() 按此增长率,计算
按此增长率,计算![]() 年投资额能否达到
年投资额能否达到![]() 万?
万?
查看答案和解析>>
科目:初中数学 来源: 题型:
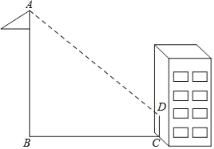
【题目】数学兴趣小组的同学们,想利用自己所学的数学知识测量学校旗杆的高度:下午活动时间,兴趣小组的同学们来到操场,发现旗杆的影子有一部分落在了墙上(如图所示).同学们按照以下步骤进行测量:测得小明的身高1.65米,此时其影长为2.5米;在同一时刻测量旗杆影子落在地面上的影长BC为9米,留在墙上的影高CD为2米,请你帮助兴趣小组的同学们计算旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋时节,硕果飘香,某精准扶贫项目果园上市一种有机生态水果,为帮助果园拓宽销路.欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为60千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x按0.5元的倍数上涨),当天销售利润为y元.
(1)求y与x的函数关系式;
(2)若该种水果每千克的利润不超过80%,求当天获得利润的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
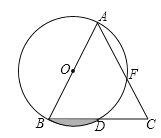
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com