
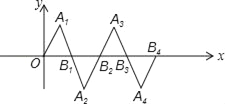
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
【答案】(4n+1,![]() )
)
【解析】
试题首先根据△OA1B1是边长为2的等边三角形,可得A1的坐标为(1,),B1的坐标为(2,0);然后根据中心对称的性质,分别求出点A2、A3、A4的坐标各是多少;最后总结出An的坐标的规律,求出A2n+1的坐标是多少即可.
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣=﹣,
∴点A2的坐标是(3,﹣),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣)=,
∴点A3的坐标是(5,),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣=﹣,
∴点A4的坐标是(7,﹣),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是,当n为偶数时,An的纵坐标是﹣,
∴顶点A2n+1的纵坐标是,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,).
故答案为:(4n+1,).


科目:初中数学 来源: 题型:
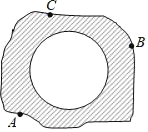
【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,他在封闭图形内划出了一个半径为1米的圆,在不远处向图形内掷石子,且记录如下:
掷石子次数石子落在的区域ABC | 50次 | 150次 | 300次 |
石子落在圆内(含圆上)的次数m | 14 | 43 | 93 |
石子落在阴影内的次数n | 19 | 85 | 186 |
(1)随着次数的增多,小明发现m与n的比值在一个常数k附近波动,请你写出k的值.
(2)请利用学过的知识求出封闭图形ABC的大致面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
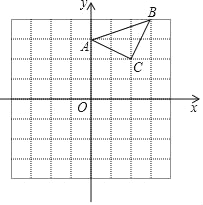
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bc+c的图象如图所示,则下列判断中错误的是( )

A. 图象的对称轴是直线x=﹣1 B. 当x>﹣1时,y随x的增大而减小
C. 当﹣3<x<1时,y<0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线与x轴交于A,B两点(点B在点A的右侧),且A,B两点的坐标分别为(-2,0),(8,0),与y轴交于点C(0,-4),连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)位于第四象限内的抛物线上是否存在点N,使得△BCN的面积最大?若存在,求出N点的坐标,及△BCN面积的最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() ,下列结论:① △APD≌△AEB;② EB⊥ED;③ 点B到直线AE的距离为
,下列结论:① △APD≌△AEB;② EB⊥ED;③ 点B到直线AE的距离为![]() ; ④
; ④![]() ,其中正确结论的序号是( )
,其中正确结论的序号是( )
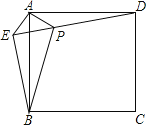
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系![]() 中,双曲线
中,双曲线![]() 与直线
与直线![]() 都经过点
都经过点![]() .
.

(1)求![]() 与
与![]() 的值;
的值;
(2)此双曲线又经过点![]() ,点
,点![]() 是
是![]() 轴的负半轴上的一点,且点
轴的负半轴上的一点,且点![]() 到
到![]() 轴的距离是2 ,联结
轴的距离是2 ,联结![]() 、
、![]() 、
、![]() ,
,
①求![]() 的面积;
的面积;
②点![]() 在
在![]() 轴上,
轴上,![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数)
是常数)
(1)求证:不论![]() 为何值,该函数图象与
为何值,该函数图象与![]() 轴一定有两个公共点。
轴一定有两个公共点。
(2)若该函数图象经过点(0,-2),则该函数图象怎样平移经过原点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com