
����Ŀ����������x�ύ��A��B����(��B�ڵ�A���Ҳ�)����A��B���������ֱ�Ϊ(-2��0)��(8��0)����y�ύ�ڵ�C(0��-4)������BC����BCΪһ������OΪ�Գ�����������BDEC����P��x���ϵ�һ�����������P������Ϊ(m��0)������P��x��Ĵ���L���������ڵ�Q����BD�ڵ�M.
(1)�������ߵĽ���ʽ��
(2)����P���߶�OB���˶�ʱ����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı���?
(3)λ�ڵ��������ڵ����������Ƿ���ڵ�N��ʹ�á�BCN��������?�����������N�������������BCN��������ֵ��������������˵������.

���𰸡�(1) �����߽���ʽΪy=![]() x2-
x2-![]() x-4��(2) ��m=4ʱ���ı���CQMD��ƽ���ı����� (3) S��BCN= 8.
x-4��(2) ��m=4ʱ���ı���CQMD��ƽ���ı����� (3) S��BCN= 8.
��������
��1���ô���ϵ����ֱ����������߽���ʽ��
��2�������εĶԳ��Կ�֪����D�����꣬���ݴ���ϵ��������ֱ��BD�Ľ���ʽ������ƽ���ı��ε����ʿɵù���m�ķ��̣����m��ֵ���ٸ���ƽ���ı��ε��ж��ɵ��ı���CQMD����״��
��3�����жϳ���N��ƽ����BC����������ֻ��һ������ʱ��λ�ã�ȷ������N�����꣬������Ͳ����������BCN�������
(1)�������ߵĽ���ʽΪy=ax2+bx+c��
��������ã�

�������߽���ʽΪy=![]() x2-
x2-![]() x-4.
x-4.
(2)��C(0��-4)��
�������εĶԳ��Կ�֪����D������Ϊ(0��4).
��ֱ��BD�Ľ���ʽΪy=kx+b'����![]() ���k=-
���k=-![]() ��b'=4.
��b'=4.
��ֱ��BD�Ľ���ʽΪy=-![]() x+4.
x+4.
��l��x�ᣬ
����M������Ϊ![]() ����Q������Ϊ
����Q������Ϊ![]() .
.
��ͼ����MQ=DCʱ���ı���CQMD��ƽ���ı��Σ�
��![]() =4-(-4).�����m2-4m=0�����m1=0(����������ȥ)��m2=4.
=4-(-4).�����m2-4m=0�����m1=0(����������ȥ)��m2=4.
����m=4ʱ���ı���CQMD��ƽ���ı���.
(3)���ڣ�����:
������Nƽ����ֱ��BC��ֱ����������ֻ��һ������ʱ����BCN��������.
��B(8��0)��C(0��-4)��
��BC=4![]() .ֱ��BC����ʽΪy=
.ֱ��BC����ʽΪy=![]() x-4�������Nƽ����ֱ��BC��ֱ��L������Ϊy=
x-4�������Nƽ����ֱ��BC��ֱ��L������Ϊy=![]() x+n����
x+n����
�������߽���ʽΪy=![]() x2-
x2-![]() x-4���������٢��ã�x2-8x-4(n+4)=0����
x-4���������٢��ã�x2-8x-4(n+4)=0����
����=64+16(n+4)=0��
��n=-8��
��ֱ��L����ʽΪy=![]() x-8����n=-8�������еã�x2-8x+16=0
x-8����n=-8�������еã�x2-8x+16=0
��x=4��
��y=-6��
��N(4��-6)��
��ͼ������N��NG��AB��

��S��BCN=S�ı���OCNG+S��MNG-S��OBC=![]() (4+6)��4+
(4+6)��4+![]() (8-4)��6-
(8-4)��6-![]() ��8��6=8.
��8��6=8.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���߳�Ϊ1�������������У�![]() ����������
����������![]() ��
��![]() ��
��![]() ���ڸ����.
���ڸ����.
��1��������![]() ����
����![]() ��ĶԳ�ͼ��
��ĶԳ�ͼ��![]() ��������
��������![]() ��
��![]() ��
��![]() �ĶԳƵ�ֱ���
�ĶԳƵ�ֱ���![]() ��
��![]() ��
��![]() ���������
������д����![]() ���ꣻ
���ꣻ
��2��![]() Ϊ
Ϊ![]() ����һ�㣬����ͼ�л���ʹ
����һ�㣬����ͼ�л���ʹ![]() ���ܳ���Сʱ�ĵ�
���ܳ���Сʱ�ĵ�![]() ����д������������ͼ�ۼ�������ֱ��д����
����д������������ͼ�ۼ�������ֱ��д����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬AC��6��BC��8������P�ӵ�A��ʼ������AC��CB��BA�˶�����P��AC��CB��BA�����˶����ٶȷֱ�Ϊÿ��3��4��5����λ��ֱ��l����AC�غϵ�λ�ÿ�ʼ����ÿ��![]() ����λ���ٶ���CB�����ƶ����ƶ������б���l��AC���ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P��һ�λص���Aʱ����P��ֱ��lͬʱֹͣ�˶���
����λ���ٶ���CB�����ƶ����ƶ������б���l��AC���ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P��һ�λص���Aʱ����P��ֱ��lͬʱֹͣ�˶���
��1����t��5��ʱ����P�߹���·����Ϊ_________����t��_________��ʱ����P���E�غϣ�
��2������P��AC�����˶�ʱ������PE��������E��AB�Ĵ��ߣ�����ΪH. ����C��P��EΪ��������������EFH���ƣ������߶�EH��ֵ��
��3������P������AC��CB��BA���˶�ʱ������P����ֱ��EF�ĶԳƵ�Q�����˶������У����γɵ��ı���PEQFΪ���Σ���t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC��������������ֱ���A��1��1����B��4��1����C��3��3����
��1������ABC����ƽ��5����λ��õ���A1B1C1���뻭����A1B1C1��
��2������ABC��ԭ��O��ʱ����ת90����õ���A2B2C2���뻭����A2B2C2��
��3���ж���O��A1��BΪ����������ε���״��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
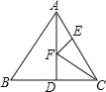
����Ŀ���ȱ���ABC �ı߳�Ϊ 4��AD �� BC ���ϵ����ߣ�F �DZ� AD �ϵĶ��㣬E �DZ� AC �ϵĵ㣬 �� AE=2���� EF+CF ȡ����Сֵʱ.
�������ܷ������ECF �Ķ�����_____��������������������գ���
����������ܣ�������ͼ�������� F��������ͼ�ۼ�����д֤����.��ֱ��д����ECF �Ķ� ����������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
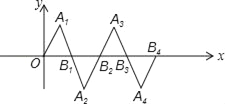
����Ŀ������ͼ��ʾ��ƽ��ֱ������ϵ�У���OA1B1�DZ߳�Ϊ2�ĵȱ������Σ�����B2A2B1����OA1B1���ڵ�B1�����ĶԳƣ�������B2A3B3����B2A2B1���ڵ�B2�����ĶԳƣ��������ȥ������B2nA2n+1B2n+1��n�����������Ķ���A2n+1��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������OΪAC���ϵ�һ������������O��ֱ��MN��BC����MN����BCA�����ƽ����CF�ڵ�F������ACB�ڽ�ƽ����CE��E��

��1����֤��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
��3����AC���ϴ��ڵ�O��ʹ�ı���AECF����������������ABC����״��֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������y=��x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y�ύ��C�㣬��P�����������ڵ�һ�����ڵ�һ�����㣬�ҵ�P�ĺ�����Ϊt��
��1���������ߵı���ʽ��
��2���������ߵĶԳ���Ϊl��l��x��Ľ���ΪD����ֱ��l���Ƿ���ڵ�M��ʹ���ı���CDPM��ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2������BC��PB��PC������PBC�����ΪS��
����S����t�ĺ�������ʽ��
����P�㵽ֱ��BC�ľ�������ֵ���������ʱ��P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
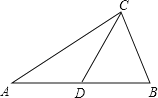
����Ŀ����ͼ��ʾ���ڡ�ABC�У�CD��AB�ϵ����ߣ���DA��DB��DC��
��1����֪��A��30�㣬���ACB�Ķ�����
��2����֪��A��40�㣬���ACB�Ķ�����
��3����֪��A��x�㣬���ACB�Ķ�����
��4��������ݽ��������ɳ�һ�����ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com