
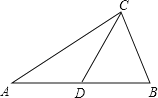
【题目】如图所示,在△ABC中,CD是AB上的中线,且DA=DB=DC.
(1)已知∠A=30°,求∠ACB的度数;
(2)已知∠A=40°,求∠ACB的度数;
(3)已知∠A=x°,求∠ACB的度数;
(4)请你根据解题结果归纳出一个结论.
【答案】(1)90°;(2)90°;(3)90°;(4)三角形中,一边上的中线等于这边的一半,那么这边所对的角等于90°.
【解析】
(1)(2)(3)利用等腰三角形及三角形内角和定理即可求出答案;
(4)三角形中,一边上的中线等于这边的一半,那么这边所对的角等于90°.
解:(1)∵在△ABC中,CD是AB上的中线,且DA=DC,∠A=30°
∴∠ACD=30°
∵∠CDB是△ACD的外角
∴∠CDB=60°
∵DB=CD
∴∠DCB=∠B=60°
∴∠ACB=∠ACD+∠DCB=30°+60°=90°;
(2)若∠A=40°,同(1),可知∠ACD=40°,∠CDB=40°+40°=80°
∠DCB=![]() (180°﹣∠CDB)=
(180°﹣∠CDB)=![]() (180°﹣80°)=50°
(180°﹣80°)=50°
∴∠ACB=∠ACD+∠DCB=40°+50°=90°;
(3)若∠A=x°,同(1),可知∠ACD=x°,∠CDB=x°+x°=2x°
∠DCB=![]() (180°﹣∠CDB)=
(180°﹣∠CDB)=![]() (180°﹣2x°)=90°﹣x°,
(180°﹣2x°)=90°﹣x°,
故∠ACB=∠ACD+∠DCB=x°+90°﹣x°=90°;
(4)三角形中,一边上的中线等于这边的一半,那么这边所对的角等于90°.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】抛物线与x轴交于A,B两点(点B在点A的右侧),且A,B两点的坐标分别为(-2,0),(8,0),与y轴交于点C(0,-4),连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)位于第四象限内的抛物线上是否存在点N,使得△BCN的面积最大?若存在,求出N点的坐标,及△BCN面积的最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
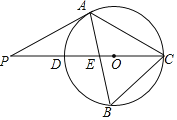
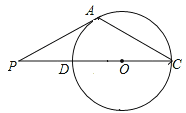
【题目】如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P.
(1)求证:∠B=2∠PCA.
(2)求证:PA是⊙O的切线;
(3)若点B位于直径CD的下方,且CD平分∠ACB,试判断此时AE与BE的大小关系,并说明由.
查看答案和解析>>
科目:初中数学 来源: 题型:
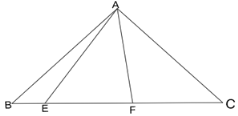
【题目】已知:如图,等腰直角三角形ABC中,∠BAC=90°,BA=AC,点E、F是线段BC上两动点且∠EAF=45°,请写出BE、EF、FC之间的等量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数)
是常数)
(1)求证:不论![]() 为何值,该函数图象与
为何值,该函数图象与![]() 轴一定有两个公共点。
轴一定有两个公共点。
(2)若该函数图象经过点(0,-2),则该函数图象怎样平移经过原点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“分式”一章后,老师写出下面的一道题让同学们解答.
计算:![]() 其中小明的解答过程如下:
其中小明的解答过程如下:
解:原式 (A)
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
(1)上述计算过程中,是从哪一步开始出现错误的?请写出该步代号:______;
(2)写出错误原因是____________;
(3)本题正确的解答过程.
解:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接五一黄金周的购物高峰,某品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣30 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)若购进乙种运动鞋x(双),要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于13000元且不超过13500元,问该专卖店有几种进货方案;
(3)在(2)的条件下求出总利润y(元)与购进乙种运动鞋x(双)的函数关系式,并用关系式说明哪种方案的利润最大,最大利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com