
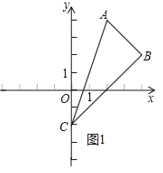
【题目】已知,如图,在平面直角坐标系![]() 中,双曲线
中,双曲线![]() 与直线
与直线![]() 都经过点
都经过点![]() .
.

(1)求![]() 与
与![]() 的值;
的值;
(2)此双曲线又经过点![]() ,点
,点![]() 是
是![]() 轴的负半轴上的一点,且点
轴的负半轴上的一点,且点![]() 到
到![]() 轴的距离是2 ,联结
轴的距离是2 ,联结![]() 、
、![]() 、
、![]() ,
,
①求![]() 的面积;
的面积;
②点![]() 在
在![]() 轴上,
轴上,![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)k=8,m=4;(2)①8;②![]()
【解析】
(1)利用一次函数图象上点的坐标特征可求出m的值,进而可得出点A的坐标,再利用反比例函数图象上点的坐标特征可求出k的值;
(2)①由(1)可得出双曲线的表达式,利用反比例函数图象上点的坐标特征可得出点B的坐标,由点C的位置可得出点C的坐标,由点A,B,C的坐标可得出AB,AC,BC的长,由AB2+BC2=AC2可得出∠ABC=90°,利用三角形的面积公式可求出△ABC的面积;
②设点E的坐标为(0,a),由点A,C的坐标可得出AC2,AE2,CE2的值,分AE=AC,CE=AC,CE=AE三种情况,可得出关于a的一元二次方程(或一元一次方程),解之即可得出结论.
解:(1)∵直线y=2x经过点A(2,m),
∴m=2×2=4,
∴点A的坐标为(2,4).
∵双曲线![]() 经过点A(2,4),
经过点A(2,4),
∴4=![]() ,
,
∴k=8.
(2)①由(1)得:双曲线的表达式为y=![]() .
.
∵双曲线y=![]() 经过点B(n,2),
经过点B(n,2),
∴2=![]() ,
,
∴n=4,
∴点B的坐标为(4,2).
∵点C是y轴的负半轴上的一点,且点C到x轴的距离是2,
∴点C的坐标为(0,2),
∴AB=![]() ,
,
BC=![]() ,
,
AC=![]() .
.
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴S△ABC=![]() ABBC=
ABBC=![]() ×
×![]() ×
×![]() =8.
=8.
②设点E的坐标为(0,a),
∴AE2=(02)2+(a4)2=a28a+20,CE2=[a(2)]2=a2+4a+4,AC2=40.
分三种情况考虑,如图2所示.
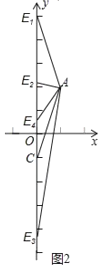
(i)当AE=AC时,a28a+20=40,
解得:a1=2(舍去),a2=10,
∴点E1的坐标为(0,10);
(ii)当CE=AC时,a2+4a+4=40,
解得:a3=2+2![]() ,a4=22
,a4=22![]() ,
,
∴点E2的坐标为(0,2+2![]() ),点E3的坐标为(0,22
),点E3的坐标为(0,22![]() );
);
(iii)当CE=AE时,a2+4a+4=a28a+20,
解得:a=![]() ,
,
∴点E4的坐标为(0,![]() ).
).
综上所述:点E的坐标为(0,10),(0,2+2![]() ),(0,22
),(0,22![]() )或(0,
)或(0,![]() ).
).


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
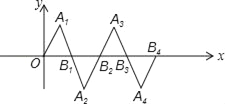
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.

(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
科目:初中数学 来源: 题型:
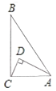
【题目】直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,AB=5cm,如果AD平分∠BAC,且AD![]() CD,那么点D到AB的距离为 ______cm.
CD,那么点D到AB的距离为 ______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数关系式;
(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,若直角
的中点,若直角![]() 绕点
绕点![]() 旋转,分别交
旋转,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则下列说法正确的个数有( )
,则下列说法正确的个数有( )
①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 的面积为一个定值,则
的面积为一个定值,则![]() 的长也是一个定值.
的长也是一个定值.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com