
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() ,下列结论:① △APD≌△AEB;② EB⊥ED;③ 点B到直线AE的距离为
,下列结论:① △APD≌△AEB;② EB⊥ED;③ 点B到直线AE的距离为![]() ; ④
; ④![]() ,其中正确结论的序号是( )
,其中正确结论的序号是( )
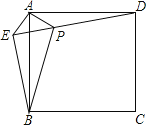
A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】B
【解析】
①利用同角的余角相等,易得∠EAB=∠PAD,再结合已知条件利用SAS可证两三角形全等;②利用①中的全等,可得∠APD=∠AEB,结合三角形的外角的性质,易得∠BEP=90°,即可证;③过B作BF⊥AE,交AE的延长线于F,利用③中的∠BEP=90°,利用勾股定理可求BE,结合△AEP是等腰直角三角形,可证△BEF是等腰直角三角形,再利用勾股定理可求EF、BF;④连接BD,求出△ABD的面积,然后减去△BDP的面积即可.
解:①∵∠EAB+∠BAP=90°,
∠PAD十∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∵在△APD和△AEB中,
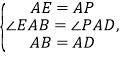
△APD≌△AEB(SAS);
故此选项成立;
②∵△APD=△AEB,
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,
∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE= 90°,
∴EB⊥ED;
故此选项成立;
③过B作BF⊥AE ,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,
又∵BE=![]() ,
,
∴BF=EF=![]() ,
,
∴点B到直线AE的距离为![]() ,
,
故此选项不正确,
④如图,连接BD,
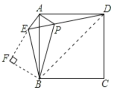
在Rt△AEP中,
∵AE=AP=1,
∴EP=![]() ,
,
又∵PB=![]() ,
,
∴BE=![]() ,
,
∵△APD≌△AEB,
∴PD=BE=![]() ,
,
∴S△ABP+S△ADP=S△ABD-S△BDP=![]() S正方形ABCD-
S正方形ABCD-![]() ×DP×BE=
×DP×BE=![]() ×(4+
×(4+![]() )-
)-![]() ×
×![]() ×
×![]() =
=![]() +
+![]() ,
,
故此选项不正确,
∴正确的有①②④,
∴B选项正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列函数中,y是x的反比例函数有( )
(1)y=3x;(2)y=﹣![]() ;(3)y=
;(3)y=![]() ;(4)﹣xy=3;(5)
;(4)﹣xy=3;(5)![]() ;(6)
;(6)![]() ;(7)y=2x﹣2;(8)
;(7)y=2x﹣2;(8)![]() .
.
A. (2)(4) B. (2)(3)(5)(8) C. (2)(7)(8) D. (1)(3)(4)(6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
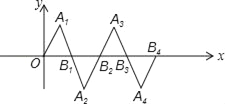
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,E 为 BC 边中点.
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD

(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.

(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com