Question

【题目】直角梯形的一个内角为，较长的腰为6，一底为5，则这个梯形的面积为（ ）

A. B. C. 25 D. 或

Answer 1

【答案】D

【解析】试题分析：根据“直角梯形的一个内角为120°，较长的腰为6cm”可求得直角梯形的高，由于一底边长为5cm不能确定是上底还是下底，故要分两种情况讨论梯形的面积，根据梯形的面积公式=（上底+下底）×高，分别计算即可．

解：根据题意可作出下图.

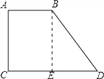
BE为高线,BE⊥CD,即∠A=∠C=90°,∠ABD=120°，BD=6cm，

∵AB∥CD,∠ABD=120°，

∴∠D=60°，

∴BE=6×sin60°=3cm; ED=6×cos60°=3cm；

当AB=5cm时,CD=5+3=8cm,梯形的面积= cm2；

当CD=5cm时,AB=53=2cm,梯形的面积= cm2；

故梯形的面积为或，

故选D.