
【题目】经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)求两辆车全部继续直行的概率.
(2)下列事件中,概率最大的是( )
A.一辆车向左转,一辆车向右转 B.两辆车都向左转
C.两辆车行驶方向相同 D.两辆车行驶方向不同
【答案】(1)![]() ,(2)D
,(2)D
【解析】
列举出所有可能出现的结果,找出两辆车全部继续直行的结果数,根据概率公式即可得答案;(2)根据(1)列举出的所有可能出现的结果,分别得出各选项的概率,即可得答案.
(1)∵所有可能出现的结果有:(直行,直行),(直行,左转),(直行,右转),(左转,直行),(左转,左转),(左转,右转),(右转,直行),(右转,左转),(右转,右转),共有9种,它们出现的可能性相同,所有的结果中,满足“两辆车全部继续直行”(记为事件A)的结果有1种,
∴P(A)=![]() .
.
(2)由(1)可知所有可能出现的结果共有9种,
A.一辆车向左转,一辆车向右转的概率为:![]()
B.两辆车都向左转的概率为:![]()
C.两辆车行驶方向相同的概率为:![]() =
=![]()
D.两辆车行驶方向不同的概率为:![]() =
=![]()
故选D.


科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
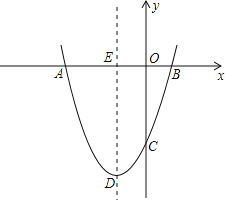
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=![]() PC.其中正确的个数是()
PC.其中正确的个数是()
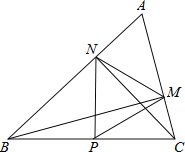
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,经过A、B、C三点的⊙O与AD相切于点A,经过点C的切线与AD的延长线相交于点P,连接AC.
(1)求证:AB=AC;
(2)若AB=4,⊙O的半径为![]() ,求PD的长.
,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次综合实践课上,同学们为教室窗户设计一个遮阳篷,小明同学绘制的设计图如图所示,其中AB表示窗户,且AB=2米,BCD表示直角遮阳蓬,已知当地一年中正午时刻太阳光与水平线CD的最小夹角∠PDN=18.6°,最大夹角∠MDN=64.5°.请你根据以上数据,帮助小明同学计算出遮阳篷中CD的长是多少米?(结果精确到0.1)(参考数据:sin18.6°≈0.32,tan18.6°≈0.34,sin64.5°≈0.90,tan64.5°≈2.1)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com