
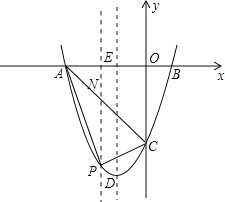
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)y=x2+2x﹣3;(2)当x=﹣![]() 时,S有最大值
时,S有最大值![]() ,此时点P的坐标为(﹣
,此时点P的坐标为(﹣![]() ,﹣
,﹣![]() );(3)点M的坐标为(0,
);(3)点M的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() )或(0,﹣1)或(0,﹣3).
)或(0,﹣1)或(0,﹣3).
【解析】
(1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式。
(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x,x2+2x﹣3),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论。
(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可。
解:(1)由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x﹣1),
将C点坐标(0,﹣3)代入,得:
a(0+3)(0﹣1)=﹣3,解得 a=1,
则y=(x+3)(x﹣1)=x2+2x﹣3,
所以抛物线的解析式为:y=x2+2x﹣3;
(2)过点P作x轴的垂线,交AC于点N.
设直线AC的解析式为y=kx+m,由题意,得
![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为:y=﹣x﹣3.
设P点坐标为(x,x2+2x﹣3),则点N的坐标为(x,﹣x﹣3),
∴PN=PE﹣NE=﹣(x2+2x﹣3)+(﹣x﹣3)=﹣x2﹣3x.
∵S△PAC=S△PAN+S△PCN,
∴S=![]() PNOA
PNOA
=![]() ×3(﹣x2﹣3x)
×3(﹣x2﹣3x)
=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,S有最大值
时,S有最大值![]() ,此时点P的坐标为(﹣
,此时点P的坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)在y轴上是存在点M,能够使得△ADM是直角三角形.理由如下:
∵y=x2+2x﹣3=y=(x+1)2﹣4,
∴顶点D的坐标为(﹣1,﹣4),
∵A(﹣3,0),
∴AD2=(﹣1+3)2+(﹣4﹣0)2=20.
设点M的坐标为(0,t),分三种情况进行讨论:
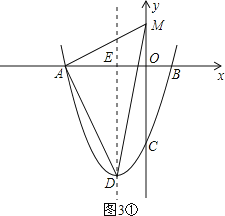
①当A为直角顶点时,如图3①,
由勾股定理,得AM2+AD2=DM2,即(0+3)2+(t﹣0)2+20=(0+1)2+(t+4)2,
解得t=![]() ,
,
所以点M的坐标为(0,![]() );
);
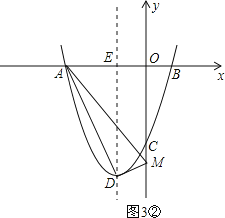
②当D为直角顶点时,如图3②,
由勾股定理,得DM2+AD2=AM2,即(0+1)2+(t+4)2+20=(0+3)2+(t﹣0)2,
解得t=﹣![]() ,
,
所以点M的坐标为(0,﹣![]() );
);
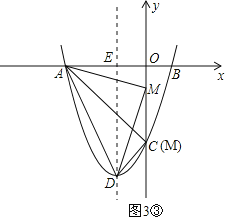
③当M为直角顶点时,如图3③,
由勾股定理,得AM2+DM2=AD2,即(0+3)2+(t﹣0)2+(0+1)2+(t+4)2=20,
解得t=﹣1或﹣3,
所以点M的坐标为(0,﹣1)或(0,﹣3);
综上可知,在y轴上存在点M,能够使得△ADM是直角三角形,此时点M的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() )或(0,﹣1)或(0,﹣3).
)或(0,﹣1)或(0,﹣3).


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译![]() 若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是
若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中, ![]() 三个顶点坐标分别为
三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ;
;
(2)将![]() 的三个顶点的横坐标与纵坐标同时乘
的三个顶点的横坐标与纵坐标同时乘![]() ,得到对应的点
,得到对应的点![]() 、
、![]() 、
、![]() ,请画出
,请画出![]()
![]() ;
;
(3)求![]() 与
与![]() 的面积比,即
的面积比,即![]() :
:![]() =________(不写解答过程,直接写出结果).
=________(不写解答过程,直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
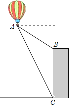
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
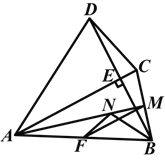
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)求两辆车全部继续直行的概率.
(2)下列事件中,概率最大的是( )
A.一辆车向左转,一辆车向右转 B.两辆车都向左转
C.两辆车行驶方向相同 D.两辆车行驶方向不同
查看答案和解析>>
科目:初中数学 来源: 题型:
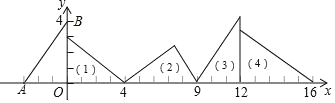
【题目】如图,在直角坐标系中,已知点 A(﹣3,0),B(0,4),对△OAB 连续作旋转变换,依次得到三角形(1),(2),(3),(4)…,则三角形(2019)的直角顶点的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com