
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
【答案】(1)A型台灯购进30盏,B型台灯购进20盏(2)要使销售这批台灯的总利润不少于1400元,至少需购进B种台灯27盏
【解析】
(1)根据题意可得等量关系:A、B两种新型节能台灯共50盏,A种新型节能台灯的台数×40+B种新型节能台灯的台数×65=2500元;设A型台灯购进x盏,B型台灯购进y盏,列方程组即可求得;
(2)根据题意可知,总利润=A种新型节能台灯的售价﹣A种新型节能台灯的进价+B种新型节能台灯的售价﹣B种新型节能台灯的进价;根据总利润不少于1400元,设购进B种台灯m盏,列不等式即可求得.
(1)设A型台灯购进x盏,B型台灯购进y盏,
根据题意,得![]() ,
,
解得:![]() ,
,
答:A型台灯购进30盏,B型台灯购进20盏;
(2)设购进B种台灯m盏,
根据题意,得利润(100﹣65)m+(60﹣40)(50﹣m)≥1400,
解得,m≥![]() ,
,
∵m是整数,
∴m≥27,
答:要使销售这批台灯的总利润不少于1400元,至少需购进B种台灯27盏.


科目:初中数学 来源: 题型:
【题目】如图所示,是某城市街道示意图,已知![]() 与
与![]() 均是等边三角形(即三条边都相等,三个角都相等的三角形),点
均是等边三角形(即三条边都相等,三个角都相等的三角形),点![]() 为公交车停靠站,且点
为公交车停靠站,且点![]() 在同一条直线上.
在同一条直线上.
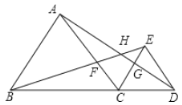
(1)图中![]() 与
与![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)连接![]() ,写出
,写出![]() 与
与![]() 的大小关系;
的大小关系;
(3)公交车甲从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站;公交车乙从
站;公交车乙从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站.若甲,乙两车分别从
站.若甲,乙两车分别从![]() 两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑白两种颜色的正方形,按如图①的方式拼图,请根据图中的信息完成下列的问题

(1)在图②中用了___________块黑色正方形,在图③中用了_____________块黑色正方形;
(2)按如图的规律继续铺下去,那么第![]() 个图形要用____________块黑色正方形;
个图形要用____________块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完![]() 块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).
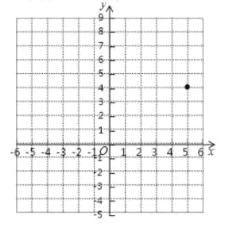
(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC 的∠ABC 的外角平分线 BD 与∠ACB 的外角平分线 CE 交于 P,过 P 作 MN∥AB 交 AC 于M,交 BC 于 N,且 AM=8,BN=5,则 MN=( )
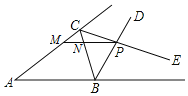
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
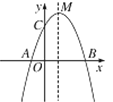
【题目】如图,已知抛物线y=-x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点M的坐标;
(2)在抛物线的对称轴上找到点P,使得△PAC的周长最小,并求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
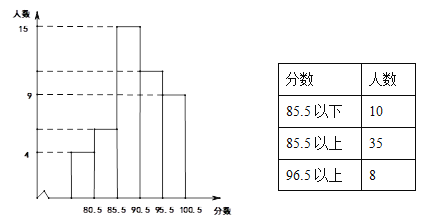
【题目】为提高公民法律意识,大力推进国家工作人员学法用法工作,今年年初某区组织本区900名教师参加“如法网”的法律知识考试,该区A学校参考教师的考试成绩绘制成如下统计图和统计表(满分100分,考试分数均为整数,其中最低分76分)
(1)求A学校参加本次考试的教师人数;
(2)若该区各学校的基本情况一致,试估计该区参考教师本次考试成绩在90.5分以下的人数;
(3)求A学校参考教师本次考试成绩85.5~96.5分之间的人数占该校参考人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“互异数”,将一个“互异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“互异数”,将一个“互异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为![]() .例如
.例如![]() =123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以
=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以![]() =6.
=6.
(1)计算![]() 和
和![]() 的值,你发现了什么规律?请用自己的语言表达;
的值,你发现了什么规律?请用自己的语言表达;
(2)若![]() =7,请直接写出
=7,请直接写出![]() 的最小值;
的最小值;
(3)若![]() ,
,![]() 都是“互异数”,其中
都是“互异数”,其中![]() ,
,![]() (1≤
(1≤![]() ≤9,1≤
≤9,1≤![]() ≤9,
≤9,![]() ,
,![]() 都是正整数),当
都是正整数),当![]() +
+![]() =16时,求
=16时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com