
【题目】如图,已知抛物线y=-x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点M的坐标;
(2)在抛物线的对称轴上找到点P,使得△PAC的周长最小,并求出点P的坐标.
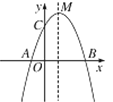
【答案】(1)M为(1,4).
(2)P(1,2).
【解析】
(1)利用B、C两点坐标求出抛物线的解析式,根据抛物线的性质得出M点坐标;
(2)根据A、B关于抛物线的对称轴对称得出AP=BP,那么△PAC的周长最小就是CPB在一条直线上,从而求出P点坐标。
(1)∵ 抛物线y = -x2+bx+c 过B(3,0)C(0,3)两点,
∴c=3, -9+3b+3=0,解得b=2 .
∴ 抛物线的解析式为![]() ,
,
顶点M为(1,4).
(2)∵ 点A、B关于抛物线的对称轴对称,
∴ 连结BC与抛物线对称轴交于一点,即为所求点P
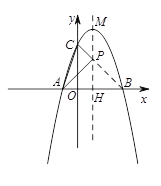
设对称轴与x轴交于点H,
∵ PH∥y轴,
∴ △PHB∽△CBO.
∴![]() .
.
由题意得BH=2,CO=3,BO=3,
∴ PH=2.
∴ P(1,2).


科目:初中数学 来源: 题型:
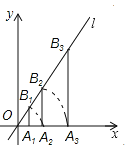
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在∠O的一边OA上.按要求画图并填空:

(1)过点A画直线AB ⊥OA,与∠O的另一边相交于点B;
(2)过点A画OB的垂线段AC,垂足为点C;
(3)过点C画直线CD∥OA ,交直线AB于点D;
(4)∠CDB= °;
(5)如果OA=8,AB=6,OB=10,则点A到直线OB的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=AC,过其中一个顶点的直线可以把这个三角形分成另外两个等腰三角形,则∠BAC( )
A. 36°,90°,![]() , 108°B. 36°,72°,
, 108°B. 36°,72°,![]() ,90°
,90°
C. 90°,72°,108°,![]() D. 36°,90°,108°,
D. 36°,90°,108°,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两图是分别由五个棱长为“1”的立方块组成的两个几何体,它们的三视图中完全一致的是
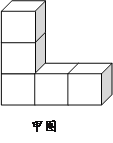
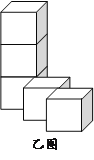
A. 三视图都一致 B. 主视图 C. 俯视图 D. 左视图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每一幅图中都有若干个大小不同的四边形,第1幅图中有1个四边形,第2幅图中有3个四边形,第3幅图中有5个四边形

(1)第4幅图中有 个四边形,第5幅图中有 个四边形;
(2)根据第1幅图到第5幅图的规律,推测第![]() 幅图中有 个四边形;(用含字母
幅图中有 个四边形;(用含字母![]() 的代数式表示)
的代数式表示)
(3)根据(2)的推测,请你计算第![]() 幅图中四边形的个数比第
幅图中四边形的个数比第![]() 幅图中四边形个数多几个?
幅图中四边形个数多几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用关于坐标系轴对称的点的坐标的特点.
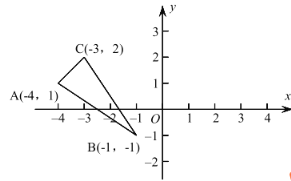
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出各点坐标:△A1( ),B1( ),C1 ( ).
(3)直接写出△ABC 的面积______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com