
【题目】如图所示,是某城市街道示意图,已知![]() 与
与![]() 均是等边三角形(即三条边都相等,三个角都相等的三角形),点
均是等边三角形(即三条边都相等,三个角都相等的三角形),点![]() 为公交车停靠站,且点
为公交车停靠站,且点![]() 在同一条直线上.
在同一条直线上.
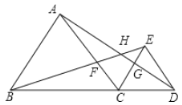
(1)图中![]() 与
与![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)连接![]() ,写出
,写出![]() 与
与![]() 的大小关系;
的大小关系;
(3)公交车甲从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站;公交车乙从
站;公交车乙从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站.若甲,乙两车分别从
站.若甲,乙两车分别从![]() 两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE⊥AC,垂足为点E,∠AGF=∠ABC,∠BFG+∠BDE=180°,
求证:BF⊥AC.
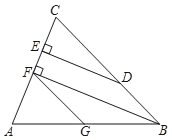
请完成下面的证明的过程,并在括号内注明理由.
证明:∵∠AGF=∠ABC(已知)
∴FG∥ ( )
∴∠BFG=∠FBC( )
∵∠BFG+∠BDE=180°(已知)
∴∠FBC+∠BDE=180°( )
∴BF∥DE( )
∴∠BFA= (两直线平行,同位角相等)
∵DE⊥AC(已知)
∴∠DEA=90°( )
∴∠BFA=90°(等量代换)
∴BF⊥AC(垂直的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() .
.

(1)若添加条件![]() ,则
,则![]() 吗?请说明理由;
吗?请说明理由;
(2)若运用“![]() ”判定
”判定![]() 与
与![]() 全等,则需添加条件:_________;
全等,则需添加条件:_________;
(3)若运用“![]() ”判定
”判定![]() 与
与![]() 全等,则需添加条件:___________.
全等,则需添加条件:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
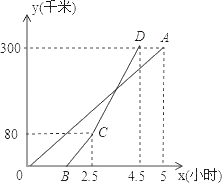
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
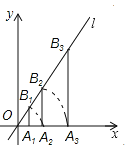
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=![]() x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则
x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则![]() 的长是_____.
的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个,黄球1个,从中任意摸出1球是黄球的概率是![]() .
.
(1)试求口袋中绿球的个数;
(2)小明第一次从口袋中任意摸出1球,不放回搅匀,第二次再摸出1球.请用列表或画树状图的方法求摸出“一绿一黄”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com