
【题目】如图,已知![]() ,
,![]() .
.

(1)若添加条件![]() ,则
,则![]() 吗?请说明理由;
吗?请说明理由;
(2)若运用“![]() ”判定
”判定![]() 与
与![]() 全等,则需添加条件:_________;
全等,则需添加条件:_________;
(3)若运用“![]() ”判定
”判定![]() 与
与![]() 全等,则需添加条件:___________.
全等,则需添加条件:___________.
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
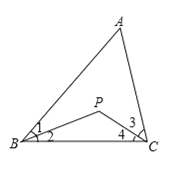
(1)当∠A=40°,∠ABC=60°时,求∠BPC的度数;
(2)当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.

(1)求BD·cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
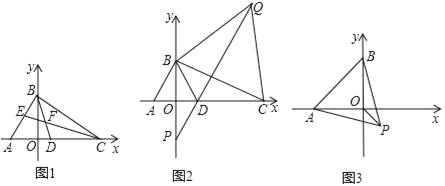
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,已知点A(m,0),B(n,0),且m,n满足(m+1)2+![]() =0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
=0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
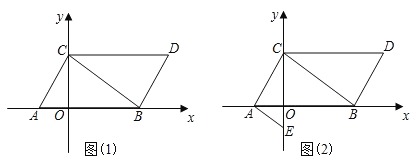
(1)求点A、B、C、D的坐标;
(2)在x轴上是否存在点P,使三角形PBC的面积等于平行四边形ABDC的面积?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),点E在y轴的负半轴上,且∠BAE=∠DCB.求证:AE∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是某城市街道示意图,已知![]() 与
与![]() 均是等边三角形(即三条边都相等,三个角都相等的三角形),点
均是等边三角形(即三条边都相等,三个角都相等的三角形),点![]() 为公交车停靠站,且点
为公交车停靠站,且点![]() 在同一条直线上.
在同一条直线上.
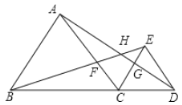
(1)图中![]() 与
与![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)连接![]() ,写出
,写出![]() 与
与![]() 的大小关系;
的大小关系;
(3)公交车甲从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站;公交车乙从
站;公交车乙从![]() 出发,按照
出发,按照![]() 的顺序到达
的顺序到达![]() 站.若甲,乙两车分别从
站.若甲,乙两车分别从![]() 两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
两站同时出发,在各站停靠的时间相同,两车的平均速度也相同,则哪一辆公交车先到达指定站?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
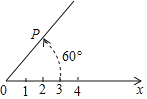
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线![]() 的解析式为y=x+1,直线
的解析式为y=x+1,直线![]() 的解析式为
的解析式为![]() ;这两个图象交于y轴上一点C,直线
;这两个图象交于y轴上一点C,直线![]() 与x轴的交点B(2,0).
与x轴的交点B(2,0).
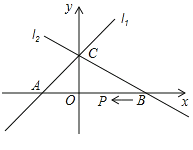
(1)求a、b的值;
(2)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com