
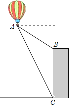
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()
科目:初中数学 来源: 题型:
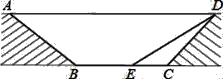
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的长;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.
(答案均精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=3,AB=8,BO=10.求:
(1)⊙O的半径;
(2)弦AC的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知α为锐角,下列结论:
(1)sinα+cosα=1;
(2)若α>45°,则sinα>cosα;
(3)如果cosα>![]() ,则α<60°;
,则α<60°;
(4)![]() =1﹣sinα.
=1﹣sinα.
其中正确结论的序号是( )
A. (1)(3)(4) B. (2)(4) C. (2)(3)(4) D. (3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
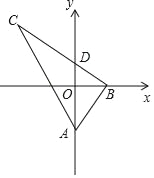
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
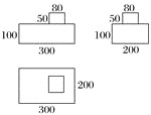
【题目】已知一个模型的三视图如图,其边长如图所示(单位:cm).制作这个模型的木料密度为150 kg/m3,则这个模型的质量是多少kg?如果油漆这个模型,每千克油漆可以漆4 m2,需要油漆多少kg?(质量=密度×体积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法:①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1∶2;④△ABC与△DEF的面积比为4∶1. 正确的个数是( )
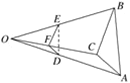
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com