
【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=![]() PC.其中正确的个数是()
PC.其中正确的个数是()
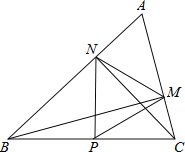
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
试题①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
∴PM=![]() BC,PN=
BC,PN=![]() BC。∴PM=PN。正确。
BC。∴PM=PN。正确。
②在△ABM与△ACN中,∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,∴![]() 。正确。
。正确。
③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,∴∠ABM=∠ACN=30°。
在△ABC中,∠BCN+∠CBM═180°﹣60°﹣30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,∴PM=PN=PB=PC。
∴∠BPN=2∠BCN,∠CPM=2∠CBM。∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°。
∴∠MPN=60°。∴△PMN是等边三角形。正确。
④当∠ABC=45°时,∵CN⊥AB于点N,∴∠BNC=90°,∠BCN=45°。∴BN=CN。
∵P为BC边的中点,∴PN⊥BC,△BPN为等腰直角三角形。
∴BN=![]() PB=
PB=![]() PC。正确。
PC。正确。
综上所述,正确的结论个数是4个。故选D。


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
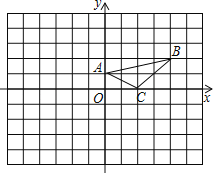
【题目】如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2,画出△A2B2C2;
(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中, ![]() 三个顶点坐标分别为
三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ;
;
(2)将![]() 的三个顶点的横坐标与纵坐标同时乘
的三个顶点的横坐标与纵坐标同时乘![]() ,得到对应的点
,得到对应的点![]() 、
、![]() 、
、![]() ,请画出
,请画出![]()
![]() ;
;
(3)求![]() 与
与![]() 的面积比,即
的面积比,即![]() :
:![]() =________(不写解答过程,直接写出结果).
=________(不写解答过程,直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
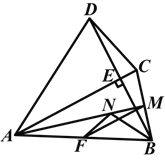
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.

(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)求两辆车全部继续直行的概率.
(2)下列事件中,概率最大的是( )
A.一辆车向左转,一辆车向右转 B.两辆车都向左转
C.两辆车行驶方向相同 D.两辆车行驶方向不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例函数y=![]() (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com