
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
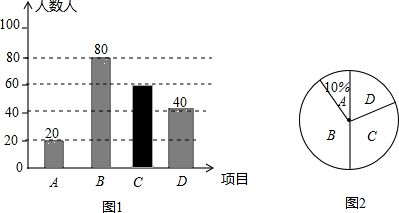
分析 ①用喜欢篮球的人数除以喜欢篮球的人数所占的百分比,即可求出这些被调查的学生数;
②先计算出羽毛球所占的百分比,再求所对应的圆心角的度数;
③根据样本估计总体,即可解答.
解答 解:①20÷10%=200(人),故①正确;
②$\frac{60}{200}×36{0}^{°}$=108°,故②正确;
③2400×$\frac{80}{200}$=960(人),故③正确;
正确的有3个,故选:D.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
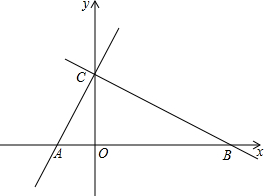 如图,直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,点A的坐标是(-$\sqrt{3}$,0),∠ABC=30°,若动点M从B点出发沿BC运动,运动的速度为每秒1个单位长度,当点M运动到C点时停止运动,设点M运动t秒时,△ABM的面积为S.
如图,直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,点A的坐标是(-$\sqrt{3}$,0),∠ABC=30°,若动点M从B点出发沿BC运动,运动的速度为每秒1个单位长度,当点M运动到C点时停止运动,设点M运动t秒时,△ABM的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
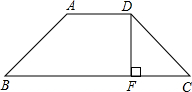 如图,四边形ABCD中,AD∥BC,且AB=CD,DF⊥BC于F,AD=DF=FC=1,将它剪两刀,剪成4块,然后拼成一个正方形,想一想,应该怎样剪?画出图形来说明.
如图,四边形ABCD中,AD∥BC,且AB=CD,DF⊥BC于F,AD=DF=FC=1,将它剪两刀,剪成4块,然后拼成一个正方形,想一想,应该怎样剪?画出图形来说明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com