【题目】如图，已知点
，
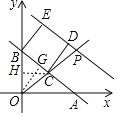
，点C是直线AB上异于点B的任一点，现以BC为一边在AB右侧作正方形BCDE，射线OC与直线DE交于点P，若点C的横坐标为m．
求直线AB的函数表达式．
若点C在第一象限，且点C为OP的中点，求m的值．
若点C为OP的三等分点
即点C分OP成1：2的两条线段
，请直接写出点C的坐标．
【答案】（1）
；（2）
；（3）
或
或
或
【解析】
（1）利用待定系数法即可解决问题；
（2）如图，作OG⊥BC于G，OH⊥OB于H．只要证明△OCG≌△CPD，利用全等三角形的性质可得OG=CD，由此构建方程即可解决问题；
（3）在第一象限和第二象限分两种情形，分别构建方程求出m即可解决问题；
解：
设直线AB的解析式为
，
把
，
代入得到
，
解得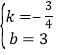
，
直线AB的解析式为．
如图，作
于G，
于H．
四边形BCDE是正方形，
，
，
，
，
≌
，
，
，
，
，
，
，
，
，
．
当点C中第一象限，
时，
∽，
：
：1，
，
，
，
，
∴C（
，
）
当点C中第一象限，
时，．
∽，
：
：2，
，
，
，
，
∴C（
，
）
当点C中第二象限，时，．
∽，
：：2，
，
，
，
，
∴C（
，
）.
当点C中第二象限，时，
∽，
：：1，
，
，
，
，
∴C（
，
）
综上所述，满足条件的点C坐标为或或或
永乾教育寒假作业快乐假期延边人民出版社系列答案科目：初中数学 来源： 题型：
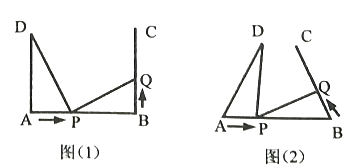
【题目】如图（1），
，
，
垂足为A，B，
，点
在线段
上以每秒2
的速度由点
向点
运动，同时点
在线段
上由点向点
运动．它们运动的时间为
（
）．
（1）
，
；（用的代数式表示）
（2）如点的运动速度与点的运动速度相等，当
时，
与
是否全等，并判断此时线段
和线段
的位置关系，请分别说明理由；
（3）如图（2），将图（1）中的“，”，改为“
”，其他条件不变．设点的运动速度为
，是否存在有理数，与是否全等？若存在，求出相应的x、t的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的优美线．
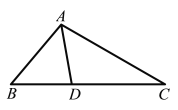
（1）如图，在△ABC中，AD为角平分线，∠B=50°，∠C=30°，求证：AD为△ABC的优美线；
（2）在△ABC中，∠B=46°，AD是△ABC的优美线，且△ABD是以AB为腰的等腰三角形，求∠BAC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市计划购进一批甲、乙两种玩具，已知
件甲种玩具的进价与
件乙种玩具的进价的和为
元，
件甲种玩具的进价与件乙种玩具的进价的和为
元．
（1）求每件甲种、乙种玩具的进价分别是多少元；
（2）如果购进甲种玩具有优惠，优惠方法是：购进甲种玩具超过
件，超出部分可以享受
折优惠，若购进
件甲种玩具需要花费
元，请你写出与的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
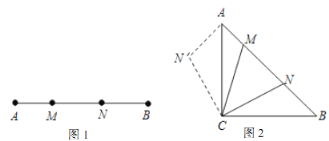
【题目】定义：如（图1），点
把线段
分割成
和
，若以
为边的三角形是一个直角三角形，则称点是线段的勾股分割点．
（1）已知点是线段的勾股分割点，若
，求的长；
（2）如（图2），在等腰直角
中， 
，点为边上两点，满足
，求证：点是线段的勾股分割点；阳阳同学在解决第（2）小题时遇到了困难，陈老师对阳阳说：要证明勾股分割点，则需设法构造直角三角形，你可以把
绕点
逆时针旋转
试一试．请根据陈老师的提示完成第（2）小题的证明过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
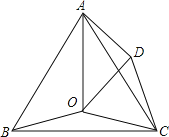
【题目】如图，O是等边三角形ABC内一点，∠AOB＝110°，∠BOC＝m°，D是△ABC外一点，且△ADC≌△BOC，连接OD．当m为_____时，△AOD是等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB＝17，BC＝21，AC＝10，动点P从点C出发，沿着CB运动，速度为每秒3个单位，到达点B时运动停止，设运动时间为t秒，请解答下列问题：
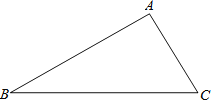
（1）求BC上的高；
（2）当t为何值时，△ACP为等腰三角形？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
