
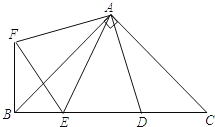
【题目】如图,RtΔABC中,AB=AC,D、E是斜边BC上两点,∠DAE=45°,将ΔADC绕点A顺时针旋转90°后,得到ΔAFB,连接EF,下列结论:①ΔAED≌ΔAEF,②![]() ,③ΔABC的面积等于四边形AFBD的面积,④
,③ΔABC的面积等于四边形AFBD的面积,④![]() ,⑤BE+DC=DE,其中正确的是( )
,⑤BE+DC=DE,其中正确的是( )
A. ①②④B. ①③④C. ③④⑤D. ①③⑤
【答案】B
【解析】
①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;
②当△ABE∽△ACD时,该比例式成立;
③根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD的面积;
④据①知BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.
⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF;由此即可确定该说法是否正确.
①根据旋转的性质知∠CAD=∠BAF,AD=AF.
∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°,∴∠EAF=45°,∴△AED≌△AEF;
故本选项正确;
②∵AB=AC,∴∠ABE=∠ACD;
∴当∠BAE=∠CAD时,△ABE∽△ACD,∴![]() ;
;
当∠BAE≠∠CAD时,△ABE与△ACD不相似,即![]() ;
;
∴此比例式不一定成立,故本选项错误;
③根据旋转的性质知△ADC≌△AFB,∴S△ABC=S△ABD+S△ABF=S四边形AFBD,即三角形ABC的面积等于四边形AFBD的面积,故本选项正确;
④∵∠FBE=45°+45°=90°,∴BE2+BF2=EF2.
∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD.
又∵EF=DE,∴BE2+DC2=DE2,故本选项正确;
⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF,∴BE+DC=BE+BF>DE=EF,即BE+DC>DE,故本选项错误.
综上所述:正确的说法是①③④.
故选B.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】一次函数 y kx b k 0的图象与反比例函数 y ![]() m 0的图象交于 A (-1,-1),B (n,2)两点.
m 0的图象交于 A (-1,-1),B (n,2)两点.
(1)求反比例函数和一次函数的表达式;
(2)点 P 在 x 轴上,过点 P 做垂直于 x 轴的直线 l,交直线 AB 于点 C,若AB=2AC,请直接写出点 C 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
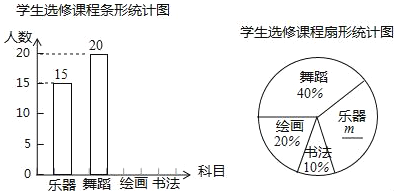
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D两点)。连接PM,过点P作PM的垂线与射线DA相交于点E(如图)。设CP=x,DE=y。
(1)写出y与x之间的函数关系式 ▲ ;
(2)若点E与点A重合,则x的值为 ▲ ;
(3)是否存在点P,使得点D关于直线PE的对称点D′落在边AB上?若存在,求x的值;若不存在,请说明理由。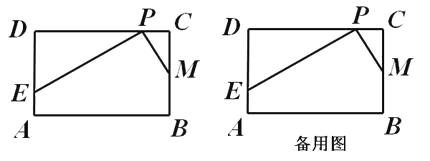
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,圆A的半径为2.下列说法中不正确的是( )
,圆A的半径为2.下列说法中不正确的是( )
A. 当![]() 时,点B在圆A上B. 当
时,点B在圆A上B. 当![]() 时,点B在圆A内
时,点B在圆A内
C. 当![]() 时,点B在圆A外D. 当
时,点B在圆A外D. 当![]() 时,点B在圆A内
时,点B在圆A内
查看答案和解析>>
科目:初中数学 来源: 题型:
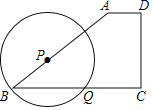
【题目】已知在梯形ABCD中,AD∥BC,AB=BC,DC⊥BC,且AD=1,DC=3,点P为边AB上一动点,以P为圆心,BP为半径的圆交边BC于点Q.
(1)求AB的长;
(2)当BQ的长为![]() 时,请通过计算说明圆P与直线DC的位置关系.
时,请通过计算说明圆P与直线DC的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是( )
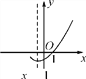
A. ①② B. ②③ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB为⊙O的直径,弦CD⊥AB于点E,在CD的延长线上取一点P,PG与⊙O相切于点G,连接AG交CD于点F.
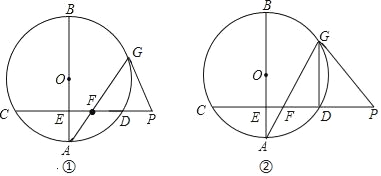
(Ⅰ)如图①,若∠A=20°,求∠GFP和∠AGP的大小;
(Ⅱ)如图②,若E为半径OA的中点,DG∥AB,且OA=2![]() ,求PF的长.
,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
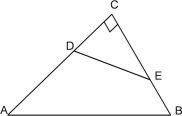
【题目】如图,在Rt△ABC中,∠C=90°,AC=16cm,AB=20cm,动点D由点C向点A以每秒1 cm速度在边AC上运动,动点E由点C向点B以每秒![]() cm速度在边BC上运动,若点D,点E从点C同时出发,运动t秒(t>0),联结DE.
cm速度在边BC上运动,若点D,点E从点C同时出发,运动t秒(t>0),联结DE.
(1)求证:△DCE∽△BCA.
(2)设经过点D、C、E三点的圆为⊙P.
①当⊙P与边AB相切时,求t的值.
②在点D、点E运动过程中,若⊙P与边AB交于点F、G(点F在点G左侧),联结CP 并延长CP交边AB于点M,当△PFM与△CDE相似时,求t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com