
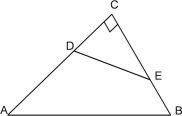
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=16cmЃЌAB=20cmЃЌЖЏЕуDгЩЕуCЯђЕуAвдУПУы1 cmЫйЖШдкБпACЩЯдЫЖЏЃЌЖЏЕуEгЩЕуCЯђЕуBвдУПУы![]() cmЫйЖШдкБпBCЩЯдЫЖЏЃЌШєЕуDЃЌЕуEДгЕуCЭЌЪБГіЗЂЃЌдЫЖЏtУы(t>0)ЃЌСЊНсDE.
cmЫйЖШдкБпBCЩЯдЫЖЏЃЌШєЕуDЃЌЕуEДгЕуCЭЌЪБГіЗЂЃЌдЫЖЏtУы(t>0)ЃЌСЊНсDE.
ЃЈ1ЃЉЧѓжЄЃКЁїDCEЁзЁїBCAЃЎ
ЃЈ2ЃЉЩшОЙ§ЕуDЁЂCЁЂEШ§ЕуЕФдВЮЊЁбP.
ЂйЕБЁбPгыБпABЯрЧаЪБЃЌЧѓtЕФжЕ.
ЂкдкЕуDЁЂЕуEдЫЖЏЙ§ГЬжаЃЌШєЁбPгыБпABНЛгкЕуFЁЂGЃЈЕуFдкЕуGзѓВрЃЉЃЌСЊНсCP ВЂбгГЄCPНЛБпABгкЕуMЃЌЕБЁїPFMгыЁїCDEЯрЫЦЪБЃЌЧѓtЕФжЕ.

ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂй![]() ЃЛЂкЕБ
ЃЛЂкЕБ![]() гы
гы![]() ЯрЫЦЪБЃЌ
ЯрЫЦЪБЃЌ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЕУЃК![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() РћгУЙДЙЩЖЈРэЧѓЕУ
РћгУЙДЙЩЖЈРэЧѓЕУ![]() ЃЌгЩ
ЃЌгЩ![]() ЃЛЕУГі
ЃЛЕУГі![]() ЃЌгж
ЃЌгж![]() ЃЌдђ
ЃЌдђ![]() Ёз
Ёз![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйСЌНс![]() ВЂбгГЄ
ВЂбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌРћгУжБНЧШ§НЧаЮЕФаББпжаЯпЕУГі
ЃЌРћгУжБНЧШ§НЧаЮЕФаББпжаЯпЕУГі![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ![]() ЃЌЕУГі
ЃЌЕУГі![]() ЃЌРћгУ
ЃЌРћгУ![]() Ёз
Ёз![]() ЃЌЕУГі
ЃЌЕУГі![]() , дйРћгУНЧЕФЕШСПЬцЛЛЕУГі
, дйРћгУНЧЕФЕШСПЬцЛЛЕУГі![]() ЃЌМД
ЃЌМД![]() ЃЌЙЪЁбPгыБп
ЃЌЙЪЁбPгыБп![]() ЯрЧаЃЌРћгУШ§НЧКЏЪ§ЧѓГіDE,CEМДПЩЧѓГіtЃЛЂкгЩЬтвтЕУ
ЯрЧаЃЌРћгУШ§НЧКЏЪ§ЧѓГіDE,CEМДПЩЧѓГіtЃЛЂкгЩЬтвтЕУ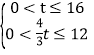 НтЕУ
НтЕУ![]() ,гЩЂйЕУ
,гЩЂйЕУ![]() ,
,![]() ЃЌ
ЃЌ![]() ЃЌЙЪ
ЃЌЙЪ![]() ,
,![]() ЃЌ
ЃЌ![]() ,дйИљОнЯрЫЦШ§НЧаЮЗжЧщПіЬжТлМДПЩЧѓНт.
,дйИљОнЯрЫЦШ§НЧаЮЗжЧщПіЬжТлМДПЩЧѓНт.
ЃЈ1ЃЉжЄУїЃКгЩЬтвтЕУЃК![]() ЃЌЁп
ЃЌЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
Ёр![]() ЃЌЁп
ЃЌЁп![]() ЃЛ
ЃЛ
Ёр![]()
гжЁп![]()
Ёр![]() Ёз
Ёз![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйСЌНс![]() ВЂбгГЄ
ВЂбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ

Ёп![]() ЃЌ
ЃЌ
ЁрDEЪЧЁб![]() ЕФжБОЖ
ЕФжБОЖ
МД![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ
Ёр![]() .
.
Ёр![]() ЃЌЁп
ЃЌЁп![]() Ёз
Ёз![]() ЃЌЁр
ЃЌЁр![]() ,
,
Ёп![]() ,Ёр
,Ёр![]()
Ёр![]() ЃЛ
ЃЛ
ЁпЁбPгыБп![]() ЯрЧаЃЌ
ЯрЧаЃЌ
ЁрЕу![]() ЮЊЧаЕуЃЌ
ЮЊЧаЕуЃЌ ![]() ЮЊЁб
ЮЊЁб![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ
Ёп![]() НтЕУ
НтЕУ![]() ЃЌЁр
ЃЌЁр![]()
![]() ЕУ
ЕУ![]() МД
МД![]() .
.
ЂкгЩЬтвтЕУ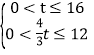 НтЕУ
НтЕУ![]() ,гЩЂйЕУ
,гЩЂйЕУ![]() ,
,![]() ЃЌ
ЃЌ![]()
Ёр,
![]() ЃЌ
ЃЌ![]() ,
,
Ёп![]()
ЁргЩ![]() гы
гы![]() ЯрЫЦПЩЕУЃК
ЯрЫЦПЩЕУЃК
ЧщПівЛЃК![]() ЕУ
ЕУ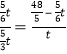 НтЕУЃК
НтЕУЃК![]() ЃЛ 0ЃМ
ЃЛ 0ЃМ![]() Ём9
Ём9
ЧщПіЖўЃК![]() ЕУ
ЕУ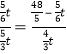 НтЕУЃК
НтЕУЃК![]() ЃЛ 0ЃМ
ЃЛ 0ЃМ![]() Ём9
Ём9
ЁрзлЩЯЫљЪіЃКЕБ![]() гы
гы![]() ЯрЫЦЪБ.
ЯрЫЦЪБ. ![]() Лђ
Лђ![]()


 ЦпВЪЬтПЈПкЫугІгУвЛЕуЭЈЯЕСаД№АИ
ЦпВЪЬтПЈПкЫугІгУвЛЕуЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtІЄABCжаЃЌAB=ACЃЌDЁЂEЪЧаББпBCЩЯСНЕуЃЌЁЯDAE=45ЁуЃЌНЋІЄADCШЦЕуAЫГЪБеыа§зЊ90ЁуКѓЃЌЕУЕНІЄAFBЃЌСЌНгEFЃЌЯТСаНсТлЃКЂйІЄAEDЁеІЄAEFЃЌЂк![]() ЃЌЂлІЄABCЕФУцЛ§ЕШгкЫФБпаЮAFBDЕФУцЛ§ЃЌЂм
ЃЌЂлІЄABCЕФУцЛ§ЕШгкЫФБпаЮAFBDЕФУцЛ§ЃЌЂм![]() ЃЌЂнBE+DC=DEЃЌЦфжае§ШЗЕФЪЧЃЈ ЃЉ
ЃЌЂнBE+DC=DEЃЌЦфжае§ШЗЕФЪЧЃЈ ЃЉ
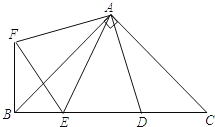
A. ЂйЂкЂмB. ЂйЂлЂмC. ЂлЂмЂнD. ЂйЂлЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФзюДѓжЕЮЊ4ЃЌЧвИУХзЮяЯпгы
ЕФзюДѓжЕЮЊ4ЃЌЧвИУХзЮяЯпгы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЌЖЅЕуЮЊ
ЃЌЖЅЕуЮЊ![]() .
.
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНМАЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЕу![]() ЪЧ
ЪЧ![]() жсЩЯЕФЖЏЕуЃЌ
жсЩЯЕФЖЏЕуЃЌ
ЂйЧѓ![]() ЕФзюДѓжЕМАЖдгІЕФЕу
ЕФзюДѓжЕМАЖдгІЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкЩш![]() ЪЧ
ЪЧ![]() жсЩЯЕФЖЏЕуЃЌШєЯпЖЮ
жсЩЯЕФЖЏЕуЃЌШєЯпЖЮ![]() гыКЏЪ§
гыКЏЪ§![]() ЕФЭМЯёжЛгавЛИіЙЋЙВЕуЃЌЧѓ
ЕФЭМЯёжЛгавЛИіЙЋЙВЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЌBC=12ЃЌвбжЊдВOЪЧЁїABCЕФЭтНгдВЃЌЧвАыОЖЮЊ10ЃЌдђBCБпЩЯЕФИпЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіе§ЖрБпаЮЕФЖдГЦжсЙВга10ЬѕЃЌЧвИУе§ЖрБпаЮЕФАыОЖЕШгк4ЃЌФЧУДИУе§ЖрБпаЮЕФБпГЄЕШгк____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃО0ЃЉгы
ЃО0ЃЉгы![]() жсНЛгкAЃЌBСНЕуЃЈAЕудкBЕуЕФзѓБпЃЉЃЌгы
жсНЛгкAЃЌBСНЕуЃЈAЕудкBЕуЕФзѓБпЃЉЃЌгы![]() жсНЛгкЕуCЁЃ
жсНЛгкЕуCЁЃ
ЃЈ1ЃЉШчЭМ1ЃЌШєЁїABCЮЊжБНЧШ§НЧаЮЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЕуPдкХзЮяЯпЩЯЃЌЕуQдкХзЮяЯпЕФЖдГЦжсЩЯЃЌШєвдBCЮЊБпЃЌвдЕуBЃЌCЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓPЕуЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуAзїжБЯпBCЕФЦНааЯпНЛХзЮяЯпгкСэвЛЕуDЃЌНЛ![]() жсНЛгкЕуEЃЌШєAE:EDЃН1:4ЃЌЧѓ
жсНЛгкЕуEЃЌШєAE:EDЃН1:4ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
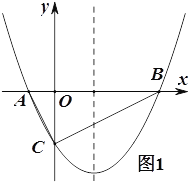
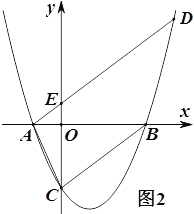
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
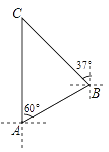
ЁОЬтФПЁПжЊЪЖИФБфЪРНчЃЌПЦММИФБфЩњЛю.ЕМКНзАБИЕФВЛЖЯИќаТМЋДѓЗНБуСЫШЫУЧЕФГіаа.ШчЭМЃЌФГаЃзщжЏбЇЩњГЫГЕЕНКкСњЬВЃЈгУCБэЪОЃЉПЊеЙЩчЛсЪЕМљЛюЖЏЃЌГЕЕНДяAЕиКѓЃЌЗЂЯжCЕиЧЁКУдкAЕиЕФе§ББЗНЯђЃЌЧвОрРыAЕи13ЧЇУзЃЌЕМКНЯдЪОГЕСОгІбиББЦЋЖЋ60ЁуЗНЯђааЪЛжСBЕиЃЌдйбиББЦЋЮї37ЁуЗНЯђааЪЛвЛЖЮОрРыВХФмЕНДяCЕиЃЌЧѓBЁЂCСНЕиЕФОрРы.ЃЈВЮПМЪ§ОнЃКsin53ЁуЁж![]() ,cos53ЁуЁж
,cos53ЁуЁж![]() ЃЌtan53ЁуЁж
ЃЌtan53ЁуЁж![]() )
)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЊЪЖБГОА
ЕБaЃО0ЧвxЃО0ЪБЃЌвђЮЊЃЈ![]() Љ
Љ![]() ЃЉ2Ён0ЃЌЫљвдxЉ2
ЃЉ2Ён0ЃЌЫљвдxЉ2![]() +
+![]() Ён0ЃЌДгЖјx+
Ён0ЃЌДгЖјx+![]() ЃЈЕБx=
ЃЈЕБx=![]() ЪБШЁЕШКХЃЉЃЎ
ЪБШЁЕШКХЃЉЃЎ
ЩшКЏЪ§y=x+![]() ЃЈaЃО0ЃЌxЃО0ЃЉЃЌгЩЩЯЪіНсТлПЩжЊЃКЕБx=
ЃЈaЃО0ЃЌxЃО0ЃЉЃЌгЩЩЯЪіНсТлПЩжЊЃКЕБx=![]() ЪБЃЌИУКЏЪ§газюаЁжЕЮЊ2
ЪБЃЌИУКЏЪ§газюаЁжЕЮЊ2![]() ЃЎ
ЃЎ
гІгУОйР§
вбжЊКЏЪ§ЮЊy1=xЃЈxЃО0ЃЉгыКЏЪ§y2=![]() ЃЈxЃО0ЃЉЃЌдђЕБx=
ЃЈxЃО0ЃЉЃЌдђЕБx=![]() =2ЪБЃЌy1+y2=x+
=2ЪБЃЌy1+y2=x+![]() газюаЁжЕЮЊ2
газюаЁжЕЮЊ2![]() =4ЃЎ
=4ЃЎ
НтОіЮЪЬт
ЃЈ1ЃЉвбжЊКЏЪ§ЮЊy1=x+3ЃЈxЃОЉ3ЃЉгыКЏЪ§y2=ЃЈx+3ЃЉ2+9ЃЈxЃОЉ3ЃЉЃЌЕБxШЁКЮжЕЪБЃЌ![]() газюаЁжЕЃПзюаЁжЕЪЧЖрЩйЃП
газюаЁжЕЃПзюаЁжЕЪЧЖрЩйЃП
ЃЈ2ЃЉвбжЊФГЩшБИзтСоЪЙгУГЩБОАќКЌвдЯТШ§ВПЗжЃКвЛЪЧЩшБИЕФАВзАЕїЪдЗбгУЃЌЙВ490дЊЃЛЖўЪЧЩшБИЕФзтСоЪЙгУЗбгУЃЌУПЬь200дЊЃЛШ§ЪЧЩшБИЕФелОЩЗбгУЃЌЫќгыЪЙгУЬьЪ§ЕФЦНЗНГЩе§БШЃЌБШР§ЯЕЪ§ЮЊ0.001ЃЎШєЩшИУЩшБИЕФзтСоЪЙгУЬьЪ§ЮЊxЬьЃЌдђЕБxШЁКЮжЕЪБЃЌИУЩшБИЦНОљУПЬьЕФзтЛѕЪЙгУГЩБОзюЕЭЃПзюЕЭЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCD жаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌвд ADЃЌODЮЊСкБпзїЦНааЫФБпаЮADOEЃЌСЌНгBE.
(1) ЧѓжЄЃКЫФБпаЮAOBEЪЧСтаЮЃЛ
(2) ШєЁЯEAO+ЁЯDCO=180ЁуЃЌDC=2ЃЌЧѓЫФБпаЮADOEЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com