
【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

【答案】(1)见解析;(2)S四边形ADOE =![]() .
.
【解析】
(1) 根据矩形的性质有OA=OB=OC=OD,根据四边形ADOE是平行四边形,得到OD∥AE,AE=OD. 等量代换得到AE=OB.即可证明四边形AOBE为平行四边形.根据有一组邻边相等的平行四边形是菱形即可证明.
(2)根据菱形的性质有∠EAB=∠BAO.根据矩形的性质有AB∥CD,根据平行线的性质有∠BAC=∠ACD,求出∠DCA=60°,求出AD=![]() .根据面积公式SΔADC,即可求解.
.根据面积公式SΔADC,即可求解.
(1)证明:∵矩形ABCD,
∴OA=OB=OC=OD.
∵平行四边形ADOE,
∴OD∥AE,AE=OD.
∴AE=OB.
∴四边形AOBE为平行四边形.
∵OA=OB,
∴四边形AOBE为菱形.
(2)解:∵菱形AOBE,
∴∠EAB=∠BAO.
∵矩形ABCD,
∴AB∥CD.
∴∠BAC=∠ACD,∠ADC=90°.
∴∠EAB=∠BAO=∠DCA.
∵∠EAO+∠DCO=180°,
∴∠DCA=60°.
∵DC=2,
∴AD=![]() .
.
∴SΔADC=![]() .
.
∴S四边形ADOE =![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).
![]()
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
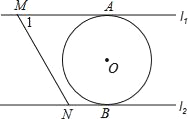
A. MN=![]() B. 若MN与⊙O相切,则AM=
B. 若MN与⊙O相切,则AM=![]()
C. l1和l2的距离为2 D. 若∠MON=90°,则MN与⊙O相切
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() 时,给出以下结论:①
时,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周长的最小值是
的周长的最小值是![]() .其中正确的是( )
.其中正确的是( )
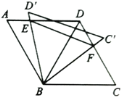
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
(1)计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
(2)小颖说:“根据实验得出,出现![]() 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
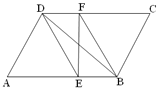
【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市某种出租车收费标准如下:乘车里程不超过3公里的一律收费10元,乘车里程超过3公里的,超过部分按每公里1.8元加收.
(1)如果有人乘该出租车行驶了8公里,那么他应付多少车费?
(2)如果该人行驶了x(x>3)公里,他应付多少车费?
(3)某游客乘出租车从A地到B地,付车费22.6元,试估算从A地到B地大约多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多![]() 小时,求自行车的平均速度?
小时,求自行车的平均速度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com