
【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
(1)计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
(2)小颖说:“根据实验得出,出现![]() 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
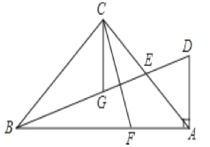
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
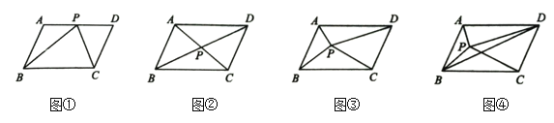
【题目】如图,四边形![]() 是面积为
是面积为![]() 的平行四边形,其中
的平行四边形,其中![]() .
.
(1)如图①,点![]() 为
为![]() 边上任意一点,则
边上任意一点,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)如图②,设![]() 交于点
交于点![]() ,则
,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是___________;
之间的数量关系是___________;
(3)如图③,点![]() 为
为![]() 内任意一点时,试猜想
内任意一点时,试猜想![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(4)如图④,已知点![]() 为
为![]() 内任意一点,
内任意一点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,仅用直尺和圆规画一个长方形,使它的面积是图中长方形面积的4倍.
(2)若新的长方形的长与宽的比为4:3,且周长为56厘米,求新长方形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上![]() 点、
点、![]() 点表示的数分别为
点表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)
在数轴上,点![]() 表示的数为-20,点
表示的数为-20,点![]() 表示的数为10,动点
表示的数为10,动点![]() 从点
从点![]() 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点![]() 也从点
也从点![]() 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时,![]() 、
、![]() 两点相遇,且动点
两点相遇,且动点![]() 、
、![]() 运动的速度之比是
运动的速度之比是![]() (速度单位:单位长度/秒).
(速度单位:单位长度/秒).
![]()
![]()
备用图
(综合运用)
(1)点![]() 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点![]() 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;
(2)当![]() 时,求运动时间;
时,求运动时间;
(3)若点![]() 、
、![]() 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也随着运动.问点
也随着运动.问点![]() 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点![]() 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
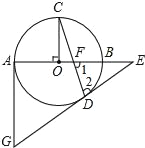
【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
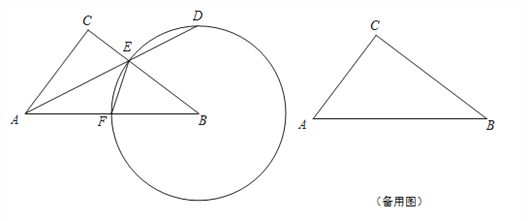
【题目】如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果![]() ,求ED的长;
,求ED的长;
(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com