
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
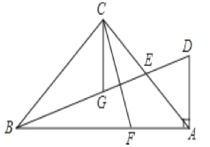
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)利用“ASA”判断△BCG≌△CFA,从而得到BG=CF;
(2)连结AG,利用等腰直角三角形的性质得CG垂直平分AB,则BG=AG,再证明∠D=∠GAD得到AG=DG,所以BG=DG,接着证明△ADE≌△CGE得到DE=GE,则BG=2DE,利用利用△BCG≌△CFA得到CF=BG,于是有CF=2DE;
(3)先得到BG=2,GE=1,则BE=3,设CE=x,则BC=AC=2CE=2x,在Rt△BCE中利用勾股定理得到x![]() +(2x)
+(2x)![]() =3
=3![]() ,解得x=
,解得x=![]() ,所以BC=
,所以BC=![]() ,AB=
,AB=![]() BC=
BC=![]() ,然后在Rt△ABD中利用勾股定理计算AD的长.
,然后在Rt△ABD中利用勾股定理计算AD的长.
(1)证明:∵∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠CAF=∠ACG=45°,
∵CG平分∠ACB,
∴∠BCG=45°,
在△BCG和△CFA中
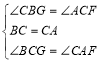 ,
,
∴△BCG≌△CFA,
∴BG=CF;
(2)证明:连结AG,
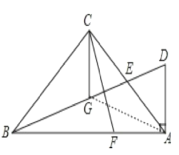
∵CG为等腰直角三角形ACB的顶角的平分线,
∴CG垂直平分AB,
∴BG=AG,
∴∠GBA=∠GAB,
∵AD⊥AB,
∴∠D+∠DBA=90°,∠GAD+∠GAB=90°,
∴∠D=∠GAD,
∴AG=DG,
∴BG=DG,
∵CG⊥AB,DA⊥AB,
∴CG∥AD,
∴∠DAE=∠GCE,
∵E为AC边的中点,
∴AE=CE,
在△ADE和△CGE中
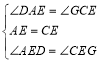 ,
,
∴△ADE≌△CGE,
∴DE=GE,
∴DG=2DE,
∴BG=2DE,
∵△BCG≌△CFA,
∴CF=BG,
∴CF=2DE;
(3)∵DE=1,
∴BG=2,GE=1,即BE=3,
设CE=x,则BC=AC=2CE=2x,
在Rt△BCE中,x![]() +(2x)
+(2x) ![]() =3
=3![]() ,解得x=
,解得x=![]() ,
,
∴BC=![]() ,
,
∴AB=![]() BC=
BC=![]() ,
,
在Rt△ABD中,∵BD=4,AB=![]() ,
,
∴AD=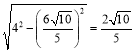 .
.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.
(1)求点C的坐标(用含a的代数式表示);
(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;
(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
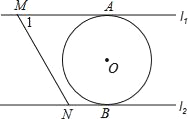
A. MN=![]() B. 若MN与⊙O相切,则AM=
B. 若MN与⊙O相切,则AM=![]()
C. l1和l2的距离为2 D. 若∠MON=90°,则MN与⊙O相切
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个几何体是由若干个棱长为3cm的小正方体搭成的,从左面、上面看到的几何体的形状图如图所示:
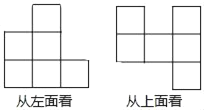
(1)该几何体最少由 个小立方体组成,最多由 个小立方体组成.
(2)将该几何体的形状固定好,
①求该几何体体积的最大值;
②若要给体积最小时的几何体表面涂上油漆,求所涂油漆面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() 时,给出以下结论:①
时,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周长的最小值是
的周长的最小值是![]() .其中正确的是( )
.其中正确的是( )
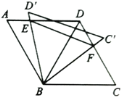
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
(1)计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
(2)小颖说:“根据实验得出,出现![]() 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
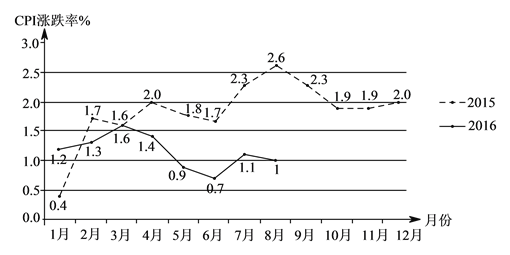
【题目】![]() 指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况.
指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况. ![]() 的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市
的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市![]() 年与
年与![]() 年
年![]() 涨跌率的统计图中的信息,请判断
涨跌率的统计图中的信息,请判断![]() 年
年![]() ~
~![]() 月份与
月份与![]() 年
年![]() ~
~![]() 月份,同月份比较
月份,同月份比较![]() 涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市
涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市![]() 年第四季度
年第四季度![]() 涨跌率变化趋势是__________,你的预估理由是__________;
涨跌率变化趋势是__________,你的预估理由是__________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com