
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
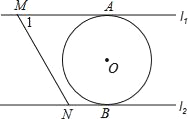
A. MN=![]() B. 若MN与⊙O相切,则AM=
B. 若MN与⊙O相切,则AM=![]()
C. l1和l2的距离为2 D. 若∠MON=90°,则MN与⊙O相切
【答案】B
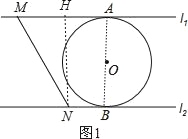
【解析】连结OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;故C正确,
作NH⊥AM于H,如图1,
则MH=AB=2,
∵∠AMN=60°,
∴sin60°=![]() ,
,
∴MN=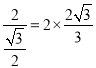 =
=![]() ;故A正确,
;故A正确,
当MN与⊙O相切,如图2,连结OM,ON,
当MN在AB左侧时,∠AMO=![]() ∠AMN=
∠AMN=![]() ×60°=30°,
×60°=30°,
在Rt△AMO中,tan∠AMO=![]() ,即AM=
,即AM=![]() =
=![]() ,
,
在Rt△OBN中,∠ONB=∠BNM=60°,tan∠ONB=![]() ,即BN=
,即BN=![]() =
=![]() ,
,
当MN在AB右侧时,AM=![]() ,
,
∴AM的长为![]() 或
或![]() ;故B错误,
;故B错误,
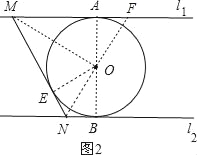
当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,如图2,
∵OA=OB,
∴Rt△OAF≌Rt△OBN,
∴OF=ON,
∴MO垂直平分NF,
∴OM平分∠NMF,
∴OE=OA,
∴MN为⊙O的切线.故D正确.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() =______,
=______,![]() =______;
=______;
(2)根据函数图象可知,当![]() 时,
时,![]() 的取值范围是____________.
的取值范围是____________.
(3)求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
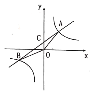
【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).
(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从扬州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为60km/h,B车的平均速度为A车的1.5倍,且走完全程B车所需时间比A车少45分钟.
(1)求扬州至南京的铁路里程;
(2)若两车以各自的平均速度分别从扬州、南京同时相向而行,问经过多少时间两车相距15km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
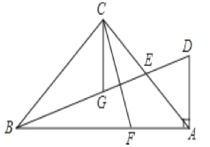
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
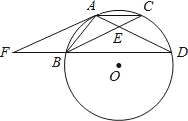
【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=![]() ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=![]() BD,连接AF.
BD,连接AF.
(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.
(1)已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,求∠MON的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com