
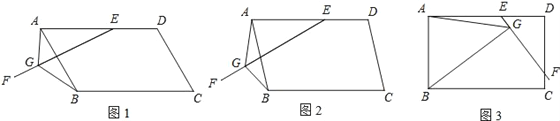
【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
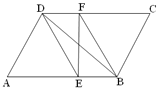
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】试题分析:(1)首先作![]() 交
交![]() 于点H,易证得
于点H,易证得![]() ≌
≌![]() ,又由
,又由![]() ,可证得
,可证得![]() 是等边三角形,继而证得结论;
是等边三角形,继而证得结论;
(2)首先作![]() 交
交![]() 于点H,作
于点H,作![]() 于点
于点![]() ,易证得
,易证得
![]() ≌
≌![]() ,又由
,又由![]() 易得
易得![]() ,继而证得结论;
,继而证得结论;
(3)首先作![]() 交
交![]() 于点H,易证得
于点H,易证得![]() ≌
≌![]() ,继而可得
,继而可得![]() 是等腰直角三角形,则可求得答案.
是等腰直角三角形,则可求得答案.
试题解析:(1)证明:如图,作∠GAH=∠EAB交GE于点H.
∴∠GAB=∠HAE.
∵∠EAB=∠EGB,∠APE=∠BPG,
∴∠ABG=∠AEH.
在△ABG和△AEH中,

∴![]() ≌
≌![]() (ASA).
(ASA).
∴BG=EH,AG=AH.
![]()
∴△AGH是等边三角形,
∴AG=HG.
∴EG=AG+BG.
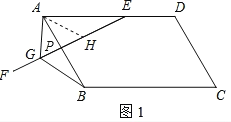
(2)如图,作∠GAH=∠EAB交GE于点H.作AM⊥EG于点M,
∴∠GAB=∠HAE.
∵∠EAB=∠EGB,∠APE=∠BPG,
∴∠ABG=∠AEH.
在△ABG和△AEH中,

∴![]() ≌
≌![]() (ASA).
(ASA).
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=α,
![]()
![]() ∴EG=GH+BG.
∴EG=GH+BG.
![]()

(3) ![]()
如图,作∠GAH=∠EAB交GE于点H.
∴∠GAB=∠HAE.
![]()
![]()
∴∠ABG=∠AEH.
∵又AB=AE,
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
![]()
∴△AGH是等腰直角三角形.
![]()
![]()



 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
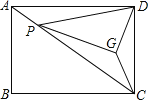
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转使∠DPG=∠DAC,且过D作DG⊥PG,连接CG,则CG最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).
![]()
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,下列条件中,不能判断梯形ABCD是等腰梯形的是( )
A. ∠ABC=∠DCB B. ∠DBC=∠ACB C. ∠DAC=∠DBC D. ∠ACD=∠DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
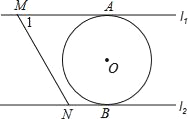
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
A. MN=![]() B. 若MN与⊙O相切,则AM=
B. 若MN与⊙O相切,则AM=![]()
C. l1和l2的距离为2 D. 若∠MON=90°,则MN与⊙O相切
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com