
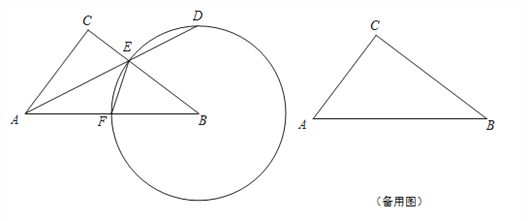
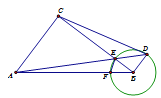
【题目】如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果![]() ,求ED的长;
,求ED的长;
(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.
【答案】(1)![]() (0<x<8);(2)ED=
(0<x<8);(2)ED=![]() ;(3)四边形ABDC不可能为直角梯形.
;(3)四边形ABDC不可能为直角梯形.
【解析】试题分析:(1)在Rt△ABC中由勾股定理得到AB=10.过E作EH⊥AB,垂足是H,易得:EH= ![]() ,BH=
,BH= ![]() ,FH=
,FH= ![]() .在Rt△EHF中,由勾股定理即可得到结论;
.在Rt△EHF中,由勾股定理即可得到结论;
(2)取弧ED的中点P,联结BP交ED于点G.由![]() ,P是弧ED的中点,得到弧EP=弧EF=弧PD,进而得到∠FBE =∠EBP =∠PBD.由垂径定理得BG⊥ED,ED =2EG =2DG.易证△BEH≌△BEG,得到EH=EG=GD=
,P是弧ED的中点,得到弧EP=弧EF=弧PD,进而得到∠FBE =∠EBP =∠PBD.由垂径定理得BG⊥ED,ED =2EG =2DG.易证△BEH≌△BEG,得到EH=EG=GD= ![]() .解Rt△CEA得到CE,BE的长,从而得到结论.
.解Rt△CEA得到CE,BE的长,从而得到结论.
(3)四边形ABDC不可能为直角梯形.分两种情况讨论:①当CD∥AB时,如果四边形ABDC是直角梯形,只可能∠ABD =∠CDB = 90o.由![]() ,即可得到结论.
,即可得到结论.
②当AC∥BD时,如果四边形ABDC是直角梯形,只可能∠ACD =∠CDB = 90o.由∠ABD> 90o.即可得到结论.
试题解析:解:(1)在Rt△ABC中,AC=6,BC=8,∠ACB=90°,∴AB=10.
过E作EH⊥AB,垂足是H,易得:EH= ![]() ,BH=
,BH= ![]() ,FH=
,FH= ![]() .
.
在Rt△EHF中, ![]() ,∴
,∴![]() (0<x<8).
(0<x<8).
(2)取弧ED的中点P,联结BP交ED于点G.
∵![]() ,P是弧ED的中点,∴弧EP=弧EF=弧PD,∴∠FBE =∠EBP =∠PBD.
,P是弧ED的中点,∴弧EP=弧EF=弧PD,∴∠FBE =∠EBP =∠PBD.
∵弧EP=弧EF ,BP过圆心,∴BG⊥ED,ED =2EG =2DG.
又∵∠CEA =∠DEB,∴∠CAE=∠EBP=∠ABC.
又∵BE是公共边,∴△BEH≌△BEG,∴EH=EG=GD= ![]() .
.
在Rt△CEA中,∵AC = 6,BC=8,tan∠CAE=tan∠ABC=![]() ,∴CE=ACtan∠CAE=
,∴CE=ACtan∠CAE=![]() =
=![]() ,∴BE=
,∴BE=![]() =
=![]() ,∴ED=2EG=
,∴ED=2EG= ![]() =
=![]() =
=![]() .
.
(3)四边形ABDC不可能为直角梯形.
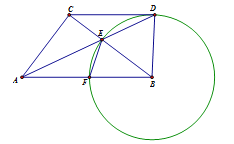
①当CD∥AB时,如果四边形ABDC是直角梯形,只可能∠ABD =∠CDB = 90o.
在Rt△CBD中,∵BC=8,∴CDcos∠BCD=![]() ,BD=BCsin∠BCD=
,BD=BCsin∠BCD=![]() =BE,∴
=BE,∴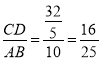 ,
, 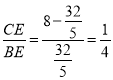 ,∴
,∴![]() ,∴CD不平行于AB,与CD∥AB矛盾,∴四边形ABDC不可能为直角梯形.
,∴CD不平行于AB,与CD∥AB矛盾,∴四边形ABDC不可能为直角梯形.
②当AC∥BD时,如果四边形ABDC是直角梯形,只可能∠ACD =∠CDB = 90o.
∵AC∥BD,∠ACB = 90o,∴∠ACB =∠CBD = 90o,∴∠ABD =∠ACB +∠BCD > 90o.
与∠ACD =∠CDB = 90o矛盾.
∴四边形ABDC不可能为直角梯形.


科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
(1)计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
(2)小颖说:“根据实验得出,出现![]() 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况.
指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况. ![]() 的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市
的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市![]() 年与
年与![]() 年
年![]() 涨跌率的统计图中的信息,请判断
涨跌率的统计图中的信息,请判断![]() 年
年![]() ~
~![]() 月份与
月份与![]() 年
年![]() ~
~![]() 月份,同月份比较
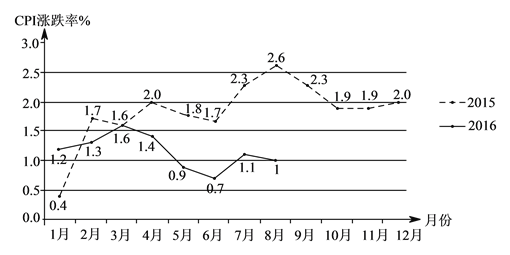
月份,同月份比较![]() 涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市
涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市![]() 年第四季度
年第四季度![]() 涨跌率变化趋势是__________,你的预估理由是__________;
涨跌率变化趋势是__________,你的预估理由是__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】准备两张同样大小的正方形纸片.
(1)取准备好的一张正方形纸片,将它的四周各剪去一个同样大小的正方形(如图1),再折合成一个无盖的长方体盒子.做成的长方体盒子的底面的边长为6cm,容积为108cm3,那么原正方形纸片的边长为多少?
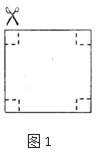
(2)取准备好的另一张一样的正方形纸片,这张纸片恰好可做成圆柱形食品罐侧面的包装纸(如图2,不计接口部分),求这个食品罐的底面圆的半径?(结果保留![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多![]() 小时,求自行车的平均速度?
小时,求自行车的平均速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
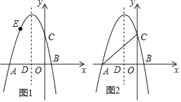
【题目】如图,抛物线y=﹣x2+bx+c的图象与x轴交于A(﹣5,0),B(1,0)两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求抛物线的函数表达式;
(2)如图1,点E(x,y)为抛物线上一点,且﹣5<x<﹣2,过点E作EF∥x轴,交抛物线的对称轴于点F,作EH⊥x轴于点H,得到矩形EHDF,求矩形EHDF周长的最大值;
(3)如图2,点P为抛物线对称轴上一点,是否存在点P,使以点P,A,C为顶点的三角形是直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
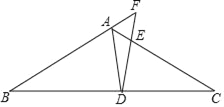
【题目】如图,在△ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且AD2=DEDF.
(1)求证:△BFD∽△CAD;
(2)求证:BFDE=ABAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有5张桌子时,两种摆放方式各能坐多少人?
(2)当有n张桌子时,两种摆放方式各能坐多少人?
(3)新学期有200人在学校就餐,但餐厅只有60张这样的餐桌,若你是老师,你打算选择哪种方式来摆放餐桌?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com