
【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
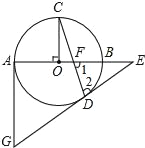
【答案】(1)证明见解析(2)6
【解析】试题分析:(1)连接OD,因为DE为⊙O的切线,所以OD⊥DE,又OC⊥OB,然后根据互余的关系可证∠1=∠2;(2)由(1)中∠1=∠2可得EF=ED,设DE=x,在Rt△ODE中,由勾股定理求得x =4,然后证Rt△EOD∽Rt△EGA.可求出AG的长.
试题解析:(1)证明:如图,连接OD,
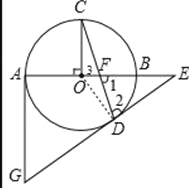
∵DE为⊙O的切线,∴OD⊥DE.∴∠ODE=90°,即∠2 ∠ODC=90°,∵OC=OD,∴∠C=∠ODC.∴∠2 ∠C=90°.∵OC⊥OB,∴∠C ∠3=90°.∴∠2=∠3,∵∠1=∠3,∴∠1=∠2.
(2)∵OF:OB=1:3,⊙O的半径为3,∴OF=1.∵∠1=∠2,∴EF=ED,在Rt△ODE中,OD=3,设DE=x,则EF=x,OE=1+x,所以![]() ,解得x =4.∴DE=4,OE=5.
,解得x =4.∴DE=4,OE=5.
∵AG为⊙O的切线,∴AG⊥AE.∴∠GAE=90°.∴∠ODE=∠GAE,∵∠OED=∠GEA,∴Rt△EOD∽Rt△EGA. ![]() 解得AG=6.
解得AG=6.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.
(1)求点C的坐标(用含a的代数式表示);
(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;
(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
(1)计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
(2)小颖说:“根据实验得出,出现![]() 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别表示使用一种白炽灯和一种节能灯的费用
分别表示使用一种白炽灯和一种节能灯的费用![]() (费用
(费用![]() 灯的售价
灯的售价![]() 电费,单位:元)与照明时间
电费,单位:元)与照明时间![]() (小时)的函数图象,假设两种灯的使用寿命都是
(小时)的函数图象,假设两种灯的使用寿命都是![]() 小时,照明效果一样.
小时,照明效果一样.
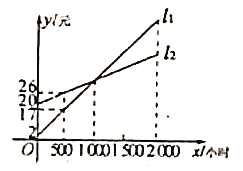
(1)根据图象分别求出![]() ,
,![]() 的函数表达式;
的函数表达式;
(2)小亮认为节能灯一定比白炽灯省钱,你是如何想的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市某种出租车收费标准如下:乘车里程不超过3公里的一律收费10元,乘车里程超过3公里的,超过部分按每公里1.8元加收.
(1)如果有人乘该出租车行驶了8公里,那么他应付多少车费?
(2)如果该人行驶了x(x>3)公里,他应付多少车费?
(3)某游客乘出租车从A地到B地,付车费22.6元,试估算从A地到B地大约多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况.
指居民消费价格指数,反映居民家庭购买消费商品及服务的价格水平的变动情况. ![]() 的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市
的涨跌率在一定程度受到季节性因素和天气因素的影响.根据北京市![]() 年与
年与![]() 年
年![]() 涨跌率的统计图中的信息,请判断
涨跌率的统计图中的信息,请判断![]() 年
年![]() ~
~![]() 月份与
月份与![]() 年
年![]() ~
~![]() 月份,同月份比较
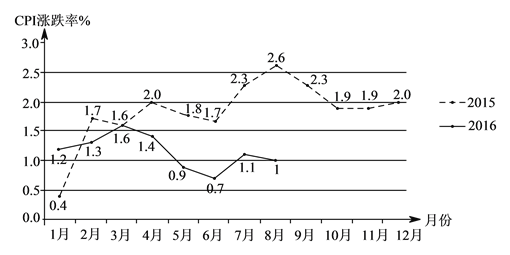
月份,同月份比较![]() 涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市
涨跌率下降最多的月份是__________月;请根据图中提供的信息,预估北京市![]() 年第四季度
年第四季度![]() 涨跌率变化趋势是__________,你的预估理由是__________;
涨跌率变化趋势是__________,你的预估理由是__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】准备两张同样大小的正方形纸片.
(1)取准备好的一张正方形纸片,将它的四周各剪去一个同样大小的正方形(如图1),再折合成一个无盖的长方体盒子.做成的长方体盒子的底面的边长为6cm,容积为108cm3,那么原正方形纸片的边长为多少?
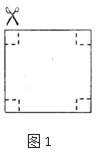
(2)取准备好的另一张一样的正方形纸片,这张纸片恰好可做成圆柱形食品罐侧面的包装纸(如图2,不计接口部分),求这个食品罐的底面圆的半径?(结果保留![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
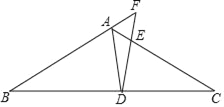
【题目】如图,在△ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且AD2=DEDF.
(1)求证:△BFD∽△CAD;
(2)求证:BFDE=ABAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com