
【题目】如图,![]() ,
,![]() 分别表示使用一种白炽灯和一种节能灯的费用
分别表示使用一种白炽灯和一种节能灯的费用![]() (费用
(费用![]() 灯的售价
灯的售价![]() 电费,单位:元)与照明时间
电费,单位:元)与照明时间![]() (小时)的函数图象,假设两种灯的使用寿命都是
(小时)的函数图象,假设两种灯的使用寿命都是![]() 小时,照明效果一样.
小时,照明效果一样.
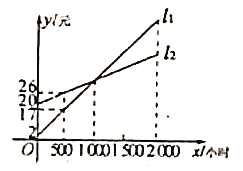
(1)根据图象分别求出![]() ,
,![]() 的函数表达式;
的函数表达式;
(2)小亮认为节能灯一定比白炽灯省钱,你是如何想的?
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在锐角![]() 内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…….照此规律,画6条不同射线,可得锐角________个.
内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…….照此规律,画6条不同射线,可得锐角________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
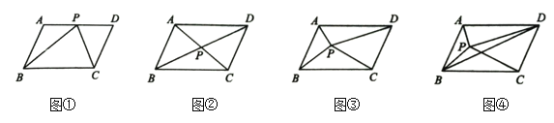
【题目】如图,四边形![]() 是面积为
是面积为![]() 的平行四边形,其中
的平行四边形,其中![]() .
.
(1)如图①,点![]() 为
为![]() 边上任意一点,则
边上任意一点,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是__________;
之间的数量关系是__________;
(2)如图②,设![]() 交于点
交于点![]() ,则
,则![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系是___________;
之间的数量关系是___________;
(3)如图③,点![]() 为
为![]() 内任意一点时,试猜想
内任意一点时,试猜想![]() 的面积
的面积![]() 和
和![]() 的面积
的面积![]() 之和与
之和与![]() 的面积
的面积![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(4)如图④,已知点![]() 为
为![]() 内任意一点,
内任意一点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,仅用直尺和圆规画一个长方形,使它的面积是图中长方形面积的4倍.
(2)若新的长方形的长与宽的比为4:3,且周长为56厘米,求新长方形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上![]() 点、
点、![]() 点表示的数分别为
点表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)
在数轴上,点![]() 表示的数为-20,点
表示的数为-20,点![]() 表示的数为10,动点
表示的数为10,动点![]() 从点
从点![]() 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点![]() 也从点
也从点![]() 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时,![]() 、
、![]() 两点相遇,且动点
两点相遇,且动点![]() 、
、![]() 运动的速度之比是
运动的速度之比是![]() (速度单位:单位长度/秒).
(速度单位:单位长度/秒).
![]()
![]()
备用图
(综合运用)
(1)点![]() 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点![]() 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;
(2)当![]() 时,求运动时间;
时,求运动时间;
(3)若点![]() 、
、![]() 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也随着运动.问点
也随着运动.问点![]() 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点![]() 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
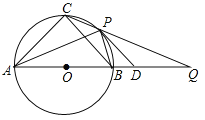
【题目】如图,等腰△ABC三个顶点在⊙O上,直径AB=12,P为弧BC上任意一点(不与B,C重合),直线CP交AB延长线与点Q,2∠PAB+∠PDA=90°,下列结论:①若∠PAB=30°,则弧BP的长为![]() ;②若PD//BC,则AP平分∠CAB;③若PB=BD,则
;②若PD//BC,则AP平分∠CAB;③若PB=BD,则![]() ,④无论点P在弧
,④无论点P在弧![]() 上的位置如何变化,CP·CQ为定值. 正确的是___________.
上的位置如何变化,CP·CQ为定值. 正确的是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
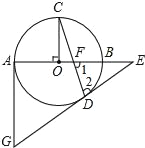
【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
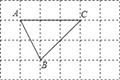
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.将线段AB绕点B顺时针旋转90°,得线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.
(Ⅰ)作出旋转后的图形;
(Ⅱ) ![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com