
【题目】已知,AB为⊙O的直径,弦CD⊥AB于点E,在CD的延长线上取一点P,PG与⊙O相切于点G,连接AG交CD于点F.
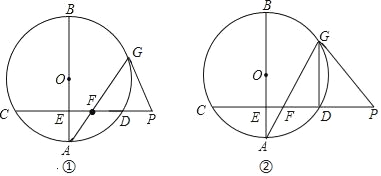
(Ⅰ)如图①,若∠A=20°,求∠GFP和∠AGP的大小;
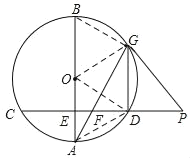
(Ⅱ)如图②,若E为半径OA的中点,DG∥AB,且OA=2![]() ,求PF的长.
,求PF的长.
【答案】(Ⅰ)∠GFP=70°,∠AGP=70°;(Ⅱ)PF=4.
【解析】
(Ⅰ)连接OG,在Rt△AEF中,∠A=20°,可得∠GFP=∠EFA=70°,因为OA=OG,所以∠OGA=∠A=20°,因为PG与⊙O相切于点G,得∠OGP=90°,可得∠AGP=90°﹣20°=70°.;
(Ⅱ)如图,连结BG,OG,OD,AD,证明△OAD为等边三角形,得∠AOD=60°,所以∠AGD=30°,因为DG∥AB,所以∠BAG=∠AGD=30°,在Rt△AGB中可求得AG=6,在Rt△AEF中可求得AF=2,再证明△GFP为等边三角形,所以PF=FG=AG﹣AF=6﹣2=4.
解:(Ⅰ)连接OG,
∵CD⊥AB于E,
∴∠AEF=90°,
∵∠A=20°,
∴∠EFA=90°﹣∠A=90°﹣20°=70°,
∴∠GFP=∠EFA=70°,
∵OA=OG,
∴∠OGA=∠A=20°,
∵PG与⊙O相切于点G,
∴∠OGP=90°,
∴∠AGP=∠OGP﹣∠OGA=90°﹣20°=70°.
(Ⅱ)如图,连结BG,OG,OD,AD,
∵E为半径OA的中点,CD⊥AB,
∴OD=AD=OA,
∴△OAD为等边三角形,
∴∠AOD=60°,
∴∠AGD=![]() ∠AOD=30°,
∠AOD=30°,
∵DG∥AB,
∴∠BAG=∠AGD=30°,
∵AB为⊙O的直径,OA=2![]() ,
,
∴∠AGB=90°,AB=4![]() ,
,
∴AG=ABcos30°=6,.
∵OG=OA,
∴∠OGA=∠BAG=30°,
∵PG与⊙O相切于点G,∴∠OGP=90°,
∴∠FGP=90°﹣30°=60°,
∵∠AEF=90°,AE=![]() ,∠BAG=30°,
,∠BAG=30°,
∴AF=2,∠GFP=∠EFA=60,
∴△GFP为等边三角形,
∴PF=FG=AG﹣AF=6﹣2=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
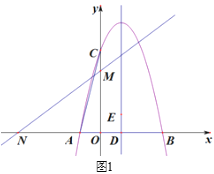
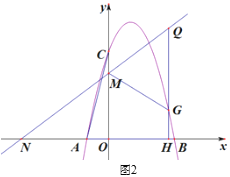
【题目】如图1,抛物线y1=![]() x2
x2![]() tx-t+2与x轴交于点A,B(点A在点B的左侧),过y轴上的点C(0,4),直线y2=kx+3交x轴,y轴于点M、N,且ON=OC.
tx-t+2与x轴交于点A,B(点A在点B的左侧),过y轴上的点C(0,4),直线y2=kx+3交x轴,y轴于点M、N,且ON=OC.
(1)求出t与k的值.
(2)抛物线的对称轴交x轴于点D,在x轴上方的对称轴上找一点E,使△BDE与△AOC相似,求出DE的长.
(3)如图2,过抛物线上动点G作GH⊥x轴于点H,交直线y2=kx+3于点Q,若点Q′是点Q关于直线MG的对称点,是否存在点G(不与点C重合),使点Q′落在y轴上?,若存在,请直接写出点G的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,RtΔABC中,AB=AC,D、E是斜边BC上两点,∠DAE=45°,将ΔADC绕点A顺时针旋转90°后,得到ΔAFB,连接EF,下列结论:①ΔAED≌ΔAEF,②![]() ,③ΔABC的面积等于四边形AFBD的面积,④
,③ΔABC的面积等于四边形AFBD的面积,④![]() ,⑤BE+DC=DE,其中正确的是( )
,⑤BE+DC=DE,其中正确的是( )
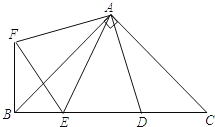
A. ①②④B. ①③④C. ③④⑤D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
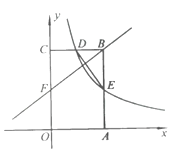
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)直接写出k的值及点E的坐标;
(2)若点F是OC边上一点,且FB⊥DE,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图像如图所示,则下列结论:①点
之间,其部分图像如图所示,则下列结论:①点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;②
;②![]() ;③
;③![]() (
(![]() 为任意实数).其中正确结论的个数是( )
为任意实数).其中正确结论的个数是( )
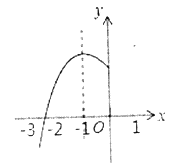
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景
当a>0且x>0时,因为(![]() ﹣
﹣![]() )2≥0,所以x﹣2
)2≥0,所以x﹣2![]() +
+![]() ≥0,从而x+
≥0,从而x+![]() (当x=
(当x=![]() 时取等号).
时取等号).
设函数y=x+![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=![]() 时,该函数有最小值为2
时,该函数有最小值为2![]() .
.
应用举例
已知函数为y1=x(x>0)与函数y2=![]() (x>0),则当x=
(x>0),则当x=![]() =2时,y1+y2=x+
=2时,y1+y2=x+![]() 有最小值为2
有最小值为2![]() =4.
=4.
解决问题
(1)已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com