
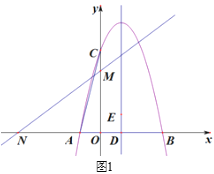
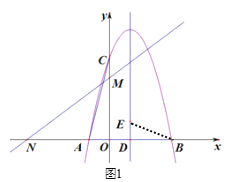
【题目】如图1,抛物线y1=![]() x2
x2![]() tx-t+2与x轴交于点A,B(点A在点B的左侧),过y轴上的点C(0,4),直线y2=kx+3交x轴,y轴于点M、N,且ON=OC.
tx-t+2与x轴交于点A,B(点A在点B的左侧),过y轴上的点C(0,4),直线y2=kx+3交x轴,y轴于点M、N,且ON=OC.
(1)求出t与k的值.
(2)抛物线的对称轴交x轴于点D,在x轴上方的对称轴上找一点E,使△BDE与△AOC相似,求出DE的长.
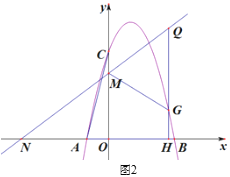
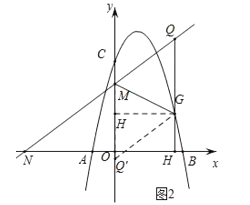
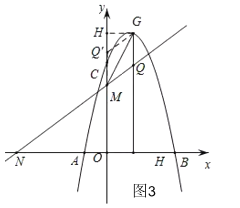
(3)如图2,过抛物线上动点G作GH⊥x轴于点H,交直线y2=kx+3于点Q,若点Q′是点Q关于直线MG的对称点,是否存在点G(不与点C重合),使点Q′落在y轴上?,若存在,请直接写出点G的横坐标;若不存在,请说明理由.
【答案】(1)t=-2,k=![]() ;(2)
;(2)![]() 或8;(3)
或8;(3)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)将C(0,4) 代入抛物线y1=![]() x2
x2![]() tx-t+2,求出t的值,由ON=OC可写出点N坐标,将其代入直线y2=kx+3即可求出k;
tx-t+2,求出t的值,由ON=OC可写出点N坐标,将其代入直线y2=kx+3即可求出k;
(2)因为∠AOC=∠EDB=90°已经确定,所以分两种情况讨论,当△AOC∽△BDE和△AOC∽△EDB时,通过对应边成比例可分别求出DE的长;
(3)先根据题意画出图形,通过轴对称的性质证明四边形QMQ'G为菱形,分别用字母表示出Q、G的坐标,分两种情况讨论求出GQ'的长度,利用三角函数可求出点G的横坐标.
解:(1)将点C(0,4)代入抛物线y1=![]() x2
x2![]() tx-t+2,得-t+2=4,∴t=-2,
tx-t+2,得-t+2=4,∴t=-2,
∴抛物线y1=![]() x2
x2![]() x+4,
x+4,
∵ON=OC,∴N(-4,0),
将N(-4,0)代入直线y2=kx+3,得-4k+3=0,∴![]() ,
,
∴直线y2=![]() x+3,
x+3,
∴t=-2,![]() .
.
(2)如图1,链接BE,在y1=![]() x2
x2![]() x+4中,当y=0时,解得:
x+4中,当y=0时,解得:![]() ,
,![]() ,
,
∴A(-1,0),B(3,0),对称轴为x=![]() ,
,
∴D(1,0),
∴AO=1,CO=4,BD=2,∠AOC=∠EDB=90°,
①当△AOC∽△BDE时,
![]() ,即
,即![]() ,
,
∴DE=8,
②当△AOC∽△EDB时,
![]() ,即
,即![]() ,
,
∴DE=![]() ,
,
综上:DE=![]() 或8;
或8;
(3)如图2,点Q'是点Q关于直线MG的对称点,且点Q'在y轴上,
由轴对称的性质知:QM= Q'M,QG= Q'G,∠Q'MG= ∠QMG,
∵QG⊥x轴,∴QG∥y轴,
∴∠Q'MG=∠QGM,
∴∠QMG=∠QGM,
∴QM=QG,
∴QM=Q'M=QG=Q'G,
∴四边形QMQ'G为菱形,
设G(a,![]() a2
a2![]() a+4),则Q(a,
a+4),则Q(a,![]() a+3),
a+3),
过点G作GH⊥y轴于点H,
∵GQ'∥QN,
∴∠GQ'H=∠NMO,
在Rt△NMO中,
NM=![]() ,
,
∴![]() ,
,
∴![]() ,
,
①当点G在直线MN下方时,QG= Q'G=![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() ;
;
②如图3,当点G在直线MN上方时,QG= Q'G=![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() .
.
综上所述:点G的横坐标为![]() ,
,![]() ,
,![]() 或
或![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
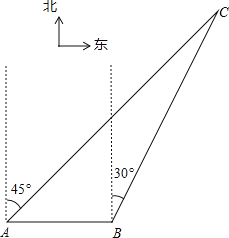
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y kx b k 0的图象与反比例函数 y ![]() m 0的图象交于 A (-1,-1),B (n,2)两点.
m 0的图象交于 A (-1,-1),B (n,2)两点.
(1)求反比例函数和一次函数的表达式;
(2)点 P 在 x 轴上,过点 P 做垂直于 x 轴的直线 l,交直线 AB 于点 C,若AB=2AC,请直接写出点 C 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
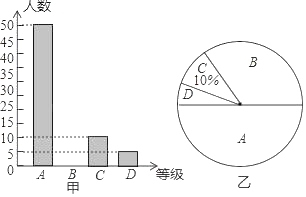
【题目】“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了 名学生进行调查;
(2)将图甲中的条形统计图补充完整;
(3)求出图乙中B等级所占圆心角的度数;
(4)根据抽样调查的结果,请你估计该校2000名学生中有多少名学生获得A等级的评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,点B分别是x轴正半轴和直线y=x(x>0)上的动点,以AB为边在右侧作矩形ABCD,AB=2,BC=1.
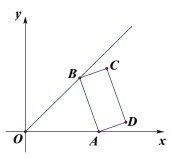
(1)若OA=![]() 时,则△ABO的面积是______;
时,则△ABO的面积是______;
(2)若点A在x轴正半轴移动时,则CO的最大距离是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度![]() 与甲盒数量
与甲盒数量![]() 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
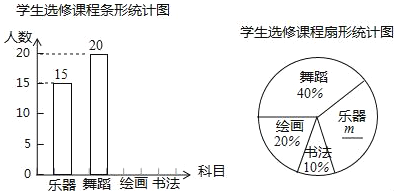
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D两点)。连接PM,过点P作PM的垂线与射线DA相交于点E(如图)。设CP=x,DE=y。
(1)写出y与x之间的函数关系式 ▲ ;
(2)若点E与点A重合,则x的值为 ▲ ;
(3)是否存在点P,使得点D关于直线PE的对称点D′落在边AB上?若存在,求x的值;若不存在,请说明理由。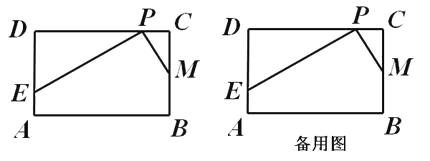
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB为⊙O的直径,弦CD⊥AB于点E,在CD的延长线上取一点P,PG与⊙O相切于点G,连接AG交CD于点F.
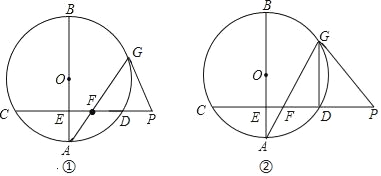
(Ⅰ)如图①,若∠A=20°,求∠GFP和∠AGP的大小;
(Ⅱ)如图②,若E为半径OA的中点,DG∥AB,且OA=2![]() ,求PF的长.
,求PF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com