
【题目】如图,在平面直角坐标系中,点A,点B分别是x轴正半轴和直线y=x(x>0)上的动点,以AB为边在右侧作矩形ABCD,AB=2,BC=1.
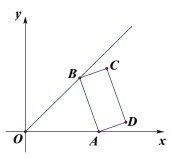
(1)若OA=![]() 时,则△ABO的面积是______;
时,则△ABO的面积是______;
(2)若点A在x轴正半轴移动时,则CO的最大距离是______.
【答案】![]()
![]()
【解析】
(1)作BE垂直OA 于E,设OE=m,则BE= m,EA=![]() ,在Rt△ABE中利用勾股定理可求得m的值,然后易求得△ABO的面积;
,在Rt△ABE中利用勾股定理可求得m的值,然后易求得△ABO的面积;
(2)如图作辅助圆和辅助线,根据圆周角定理结合等腰直接三角形的性质可得外接圆半径为![]() ,求出HB=HG=1,在Rt△HGC中求出GC=
,求出HB=HG=1,在Rt△HGC中求出GC=![]() ,只有在C、G、
,只有在C、G、![]() 共线时,OC最长,求出OC即可.
共线时,OC最长,求出OC即可.
解:(1)作BE垂直OA 于E,设OE=m,则BE= m,EA=![]() ,
,
在Rt△ABE中,![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
∴![]()
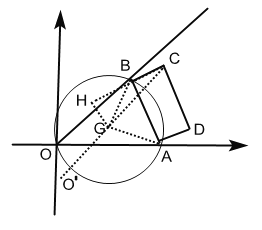
(2)因为AB为定长,∠BOA=45°,作△ABO外接圆G,圆心为G,连接GB、GA、GC、延长GC交圆G于点![]() ,
,
根据题意可知,A、B在运动的过程中可以看作是点O在△ABO外接圆G上运动,
∵∠BOA=45°,∴∠BGA=90°,∠GBC=135°,
作GH⊥CB交其延长线于H,
则∠GBH=∠HGB=45°,
∵AB=2,∴GB=![]() ,HB=HG=1,
,HB=HG=1,
在Rt△HGC中,GC=![]() ,
,![]() ,
,
只有在C、G、![]() 共线时,OC最长,
共线时,OC最长,
则![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】关于x的方程(x﹣3)(x﹣5)=m(m>0)有两个实数根α,β(α<β),则下列选项正确的是( )
A. 3<α<β<5 B. 3<α<5<β C. α<2<β<5 D. α<3且β>5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
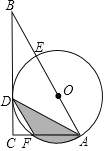
【题目】如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.若⊙O的半径为2.求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
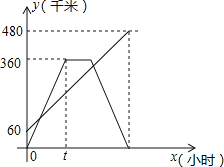
【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
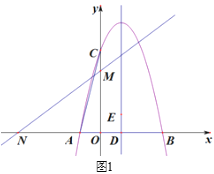
【题目】如图1,抛物线y1=![]() x2
x2![]() tx-t+2与x轴交于点A,B(点A在点B的左侧),过y轴上的点C(0,4),直线y2=kx+3交x轴,y轴于点M、N,且ON=OC.
tx-t+2与x轴交于点A,B(点A在点B的左侧),过y轴上的点C(0,4),直线y2=kx+3交x轴,y轴于点M、N,且ON=OC.
(1)求出t与k的值.
(2)抛物线的对称轴交x轴于点D,在x轴上方的对称轴上找一点E,使△BDE与△AOC相似,求出DE的长.
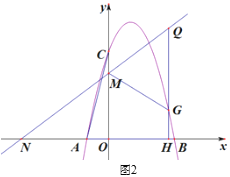
(3)如图2,过抛物线上动点G作GH⊥x轴于点H,交直线y2=kx+3于点Q,若点Q′是点Q关于直线MG的对称点,是否存在点G(不与点C重合),使点Q′落在y轴上?,若存在,请直接写出点G的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
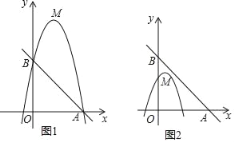
【题目】已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否在直线y=4x+1上,并说明理由.
(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.
(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(![]() ,y1),D(
,y1),D(![]() ,y2)都在二次函数图象上,试比较y1与y2的大小.
,y2)都在二次函数图象上,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
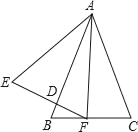
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠C;②DF=BF;③△ADE∽△FDB;④∠BFD=∠CAF.其中正确的结论是_____(填写所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com