
����Ŀ�����й��Ρ����л�����ÿһ���˵��Σ�Ҳ��ÿһ����Сѧ�����Σ�����Сѧ��չ�����ж���������ǡ��й��Ρ�������һ��������������������ѧУ�ھ����ж���У���ȫУѧ����A�����㣩��B�����ã���C���ϸ�D�����ϸ��ĸ��ȼ��������ۣ��ִ��г�ȡ���ɸ�ѧ�����е��飬���Ƴ���������������ͳ��ͼ���������ͼ����Ϣ����������⣺
��1������ȡ���� ����ѧ�����е��飻
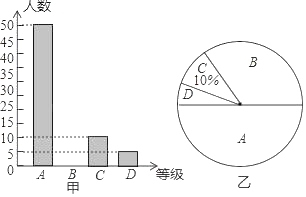
��2����ͼ���е�����ͳ��ͼ����������
��3�����ͼ����B�ȼ���ռԲ�ĽǵĶ�����
��4�����ݳ�������Ľ����������Ƹ�У2000��ѧ�����ж�����ѧ�����A�ȼ������ۣ�
���𰸡���1��100����2�������������3��126������4��������1000��ѧ�����A�ȼ������ۣ�
��������
��1����C�ȼ���������������������ռ�ٷֱȿɵõ�����������
��2�����ݸ��ȼ�����֮�͵������������B�ȼ��������ݴ˿ɲ�ȫ����ͼ��
��3����360������B�ȼ�����ռ�������ı�����
��4��������������������A�ȼ�����ռ�������ı����ɵã�
��1����ȡ�����ѧ��������Ϊ10��10%��100��
�ʴ�Ϊ��100��
��2��B�ȼ�������Ϊ100��50��10��5��35���ˣ���
������ͳ��ͼ��ͼ��
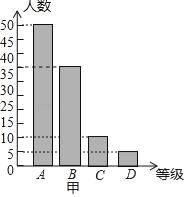
��3��ͼ����B�ȼ���ռԲ�ĽǵĶ���360���![]() ��126����
��126����
��4��2000��![]() ��1000��
��1000��
�𣺹�����1000��ѧ�����A�ȼ������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���C������Ϊ��0��-1����
��1��������ABC����ԭ��O�����ĶԳƵ�ͼ����A1B1C1��
��2���ڣ�1����������ֱ��д����A1������Ϊ______��B1������Ϊ______��
��3�������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
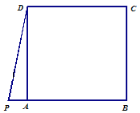
����Ŀ����ͼ�������� ABCD �У�P �� BA �ӳ�����һ�㣬��PDA ��0 45��.�� A���� E ���� DP �Գƣ����� ED��EP �����ӳ� EP ������CB �ڵ� F ������ DF .
��1���밴����ĿҪ��ȫͼ��.
��2����֤����EDF=��CDF
��3�����EDF(���� ��ʽ�ӱ�ʾ)��
��4���� P ��PH��DP�� DF �ڵ� H ������ BH �� ���� AP �� BH ��������ϵ������֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
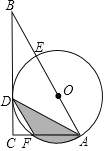
����Ŀ����ͼ����Rt��ABC�У���C=90����AB=6��AD�ǡ�BAC��ƽ���ߣ�����A��D�����Բ��Բ��Oǡ������AB�ϣ���O�ֱ���AB��AC�ཻ�ڵ�E��F������O�İ뾶Ϊ2������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
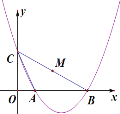
����Ŀ����ͼ��������![]() ��x���ڵ�A��B����y���ڵ�C������ABCֽƬ�ϵĵ�C���Ŵ��������˶�ʱ�����ABCֽƬ��֮Ҳ����ˮƽ�ƶ�����ֽƬ��BC���е�M����Ϊ(m��n)���ڴ��˶������У�n��m�Ĺ�ϵʽ��( )
��x���ڵ�A��B����y���ڵ�C������ABCֽƬ�ϵĵ�C���Ŵ��������˶�ʱ�����ABCֽƬ��֮Ҳ����ˮƽ�ƶ�����ֽƬ��BC���е�M����Ϊ(m��n)���ڴ��˶������У�n��m�Ĺ�ϵʽ��( )
A. n=![]() (m-
(m-![]() )2-
)2-![]() B. n=
B. n=![]() (m-
(m-![]() )2+
)2+![]()
C. n=![]() (m-
(m-![]() )2-
)2-![]() D. n=
D. n=![]() (m-
(m-![]() )2-
)2-![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
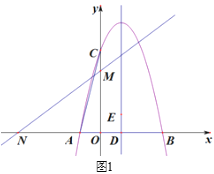
����Ŀ����ͼ1��������y1=![]() x2
x2![]() tx-t+2��x�ύ�ڵ�A��B(��A�ڵ�B�����)����y���ϵĵ�C(0��4)��ֱ��y2=kx+3��x�ᣬy���ڵ�M��N����ON=OC.
tx-t+2��x�ύ�ڵ�A��B(��A�ڵ�B�����)����y���ϵĵ�C(0��4)��ֱ��y2=kx+3��x�ᣬy���ڵ�M��N����ON=OC.
(1)���t��k��ֵ.
(2)�����ߵĶԳ��ύx���ڵ�D����x���Ϸ��ĶԳ�������һ��E��ʹ��BDE���AOC���ƣ����DE�ij�.
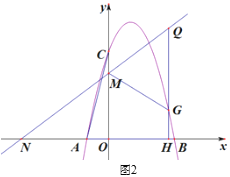
(3)��ͼ2�����������϶���G��GH��x���ڵ�H����ֱ��y2=kx+3�ڵ�Q������Q���ǵ�Q����ֱ��MG�ĶԳƵ㣬�Ƿ���ڵ�G(�����C�غ�)��ʹ��Q������y���ϣ��������ڣ���ֱ��д����G�ĺ����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������λͬѧ����һ��ƹ���������Ҫ����ѡ����λͬѧ���һ������.
��1��������״ͼ�����б�������ǡ��ѡ�мס�����λͬѧ�ĸ���.
��2������ȷ���״��һ�����ٴ�������λͬѧ�����ѡȡһλ����ǡ��ѡ����ͬѧ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
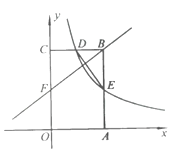
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��2��3����˫����y=![]() ��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��
��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��
��1��ֱ��д��k��ֵ����E�����ꣻ
��2������F��OC����һ�㣬��FB��DE����ֱ��FB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com