
【题目】在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为 .
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.
(1)求AB的长;
(2)求⊙O的半径.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923086297137152/1923946164551680/STEM/edc8c851f08548f08f9e61b4dab2d43e.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形.如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第3个图形中直角三角形的个数有______个,第2018个图形中直角三角形的个数有______个.
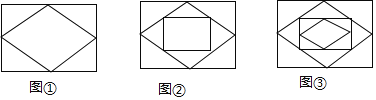
查看答案和解析>>
科目:初中数学 来源: 题型:
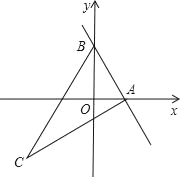
【题目】已知:如图,直线y=kx+2与x轴正半轴相交于A(t,0),与y轴相交于点B,抛物线y=﹣x2+bx+c经过点A和点B,点C在第三象象限内,且AC⊥AB,tan∠ACB=![]() .
.
(1)当t=1时,求抛物线的表达式;
(2)试用含t的代数式表示点C的坐标;
(3)如果点C在这条抛物线的对称轴上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B所表示的数分别为a和b,且满足|a+3|+(b-9)2=0,O为原点;

(1) a= ,b= .
(2) 若点C从O点出发向右运动,经过3秒后点C到A点的距离等于点C到B点距离,求点C的运动速度?(结合数轴,进行分析.)
(3) 若点D以2个单位每秒的速度从点O向右运动,同时点P从点A出发以3个单位每秒的速度向左运动,点Q从点B出发,以6个单位每秒的速度向右运动.在运动过程中,M、N分别为PD、OQ的中点,问![]() 的值是否发生变化,请说明理由.(注:PD指的是点P与D之间的线段,而算式PQ-OD指线段PQ与OD长度的差.类似的,其它的两个大写字母写在一起时意义一样 .
的值是否发生变化,请说明理由.(注:PD指的是点P与D之间的线段,而算式PQ-OD指线段PQ与OD长度的差.类似的,其它的两个大写字母写在一起时意义一样 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.
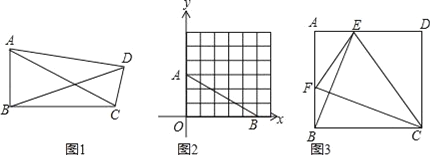
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒

当t = 4时,求线段PQ的长度
(2)当t为何值时,△PCQ是等腰三角形?
(3)当t为何值时,△PCQ的面积等于16cm2?
(4)当t为何值时,△PCQ∽△ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
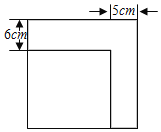
【题目】如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条.如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com