Question

【题目】阅读材料：

基本不等式≤（a＞0，b＞0），当且仅当a＝b时等号成立，它是解决最值问题的有力工具．

例如：在x＞0的条件下，当x为何值时，x+有最小值，最小值是多少？

解：∵x＞0，＞0∴≥，即≥2，∴≥2

当且仅当x＝，即x＝1时，x+有最小值，最小值为2．

请根据阅读材料解答下列问题：

（1）已知x＞0，则当x为____时，代数式3x+的最小值为______；

（2）已知a＞0，b＞0，a2+b2=7，则ab的最大值为_____

（3）已知矩形面积为9，求矩形周长的最小值．

Answer 1

【答案】（1）1，6；（2）；（3）12.

【解析】

（1）利用基本不等式即可解决问题；
（2）利用基本不等式变形式即可得解；

（3）设这个矩形的长为x米，则宽=面积÷长，即宽=米，则矩形周长为2倍的长+2倍的宽，本题就可以转化为两个非负数的和的问题，从而根据基本不等式求解．

解：（1）∵x＞0，3x>0，>0，

∴，

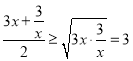即，

当且仅当3x＝，即x＝1时，3x+有最小值，最小值为6．

故答案为：1，6；

（2）由基本不等式≤（a＞0，b＞0）得

即 （a＞0，b＞0）

当且仅当a＝b时等号成立，

∵a2+b2=7，

∴

即，当且仅当a=b=时，等号成立，

故答案为：；

（3）设矩形的长为x米，宽=，矩形的周长为2（），

∵x>0，>0，

∴，

当且仅当时等号成立，即x=3时，有最小值6，2（）有最小值12

即矩形的周长的最小值为12，此时长为3，宽也为3.