
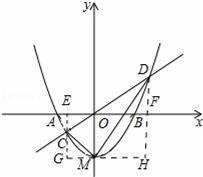
如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.

【考点】二次函数综合题.
【分析】方法一:
(1)待定系数法即可解得.
(2)由抛物线的解析式可知OA=OB=OM=1,得出∠AMO=∠MAO=∠BMO=∠MBO=45°从而得出△MAB是等腰直角三角形.
(3)分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC于G,交DF于H,设D(m,m2﹣1),C(n,n2﹣1),通过EG∥DH,得出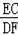
 =
=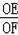
 ,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,利用对应角相等得出∠CMG+∠DMH=90°,即可求得结论.
,从而求得m、n的关系,根据m、n的关系,得出△CGM∽△MHD,利用对应角相等得出∠CMG+∠DMH=90°,即可求得结论.
方法二:
(1)略.
(2)求出A,B,M三点坐标,用勾股定理或黄金法则二证明直角,用对称性证明等腰.
(3)设CD的直线方程与抛物线联立,求出C,D参数坐标,利用黄金法则二证明垂直.
【解答】方法一:
解:(1)∵抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),
∴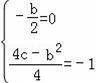
 ,解得b=0,c=﹣1,
,解得b=0,c=﹣1,
∴抛物线的解析式为:y=x2﹣1.
(2)△MAB是等腰直角三角形.
由抛物线的解析式为:y=x2﹣1可知A(﹣1,0),B(1,0),
∴OA=OB=OM=1,
∴∠AMO=∠MAO=∠BMO=∠MBO=45°,
∴∠AMB=∠AMO+∠BMO=90°,AM=BM,
∴△MAB是等腰直角三角形.
(3)MC⊥MD;
分别过C点,D点作y轴的平行线,交x轴于E、F,过M点作x轴的平行线交EC延长线于G,交DF于H,
设D(m,m2﹣1),C(n,n2﹣1),
∴OE=﹣n,CE=1﹣n2,OF=m,DF=m2﹣1,
∵OM=1,
∴CG=n2,DH=m2,
∵EG∥DH,
∴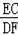
 =
=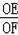
 ,
,
即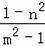
 =
=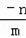
 ,
,
m(1﹣n2)=﹣n(m2﹣1),
m﹣mn2=﹣m2n+n,
(m2n﹣mn2)=﹣m+n,
mn(m﹣n)=﹣(m﹣n),
∴mn=﹣1
解得m=﹣
 ,
,
∵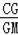
 =
=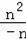
 =﹣n,
=﹣n,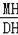
 =
=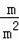
 =
=
 =﹣n,
=﹣n,
∴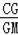
 =
=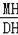
 ,
,
∵∠CGM=∠MHD=90°,
∴△CGM∽△MHD,
∴∠CMG=∠MDH,
∵∠MDH+∠DMH=90°
∴∠CMG+∠DMH=90°,
∴∠CMD=90°,
即MC⊥MD.
方法二:
(1)略.
(2)A(﹣1,0),B(1,0),M(0,﹣1),
∴KAM=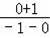
 =﹣1,KBM=
=﹣1,KBM=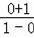
 =1,
=1,
∴KAM×KBM=﹣1,∴AM⊥BM,
又AM=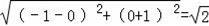
 ,
,
BM=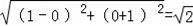
 ,
,
∴AM=BM,
∴△MAB为等腰直角三角形.
(3)当直线为x轴时,直线CD与抛物线的交点为A,B,由(2)可知CM⊥DM,设CD的直线方程为:y=kx(k≠0)
∴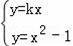
 ⇒x=
⇒x=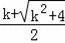
 或
或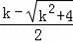
 ,
,
∴C(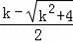
 ,
,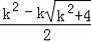
 ),D(
),D(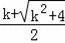
 ,
,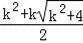
 ),
),
KCM=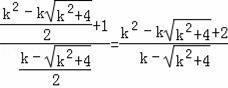
 ,
,
KDM=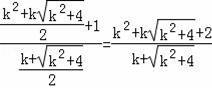
 ,
,
∴KCM×KDM=﹣1,
∴CM⊥DM.



 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
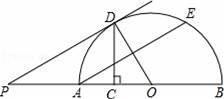
如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是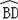
 的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
(1)填空:甲种收费的函数关系式是 .
乙种收费的函数关系式是 .
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com