
分析 根据正比例函数、反比例函数的定义,可得答案.
解答 解:设乙为a,由y-$\sqrt{2}$与乙成正比例,得
y-$\sqrt{2}$=k1a,y=k1a+$\sqrt{2}$,
由乙与$\frac{3}{x}$成反比例,得
a=$\frac{{k}_{2}}{\frac{3}{x}}$=$\frac{{k}_{2}x}{3}$.
y=$\frac{{k}_{1}{k}_{2}x}{3}$+$\sqrt{2}$,
故答案为:一次函数.
点评 本题考查了反比例函数的定义,利用了正比例函数的定义:形如y=kx (k是不等于零的常数),利用了反比例函数的定义:形如y=$\frac{k}{x}$ (k是不等于零的常数).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
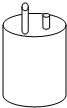 如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?
如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
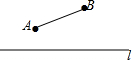 公路l同侧的A、B两村,共同出资在公路边修建一个客车停靠站C,并使停靠站到A、B两村的距离相等,你如何确定停靠站C的位置.利用尺规作图作出点C,写出作法,并保留作图痕迹.
公路l同侧的A、B两村,共同出资在公路边修建一个客车停靠站C,并使停靠站到A、B两村的距离相等,你如何确定停靠站C的位置.利用尺规作图作出点C,写出作法,并保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com