
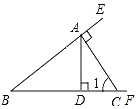
 如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:
如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:分析 根据垂直定义可得∠BAC=90°,∠ADC=∠ADB=∠CAE=90°,然后再根据余角定义和补角定义进行分析即可.
解答  解:∵CA⊥BE,
解:∵CA⊥BE,
∴∠BAC=90°,
∴∠B+∠1=90°,
∴∠1是∠B的余角,故①正确;
∵AD⊥BF,
∴∠ADC=∠ADB=90°,
∴∠B+∠BAD=90°,∠1+∠DAC=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴图中互余的角共有4对,故②正确;
∵∠1+∠ACF=180°,
∴∠1的补角是∠ACF,
∵∠1+∠DAC=90°,∠BAD+∠DAC=90°,
∴∠1=∠BAD,
∵∠BAD+∠DAE=180°,
∴∠1+∠DAE=180°,
∴∠1的补角有∠DAE,故③说法错误;
∵∠ADB=90°,∠ADC=90°,∠BAC=∠CAF=90°,
∴∠ADC,∠BAC,∠CAE和∠ADB互补,故④说法正确.
故答案为:①②④.
点评 此题主要考查了余角和补角,关键是掌握两角之和为90°时,这两个角互余;两角之和为180°时,这两个角互补.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:填空题
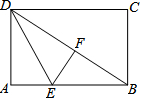 如图,折叠长方形纸片ABCD,先折出对角线BD,再将AD折叠到BD上,得到折痕DE,点A的对应点是点F,若AB=8,BC=6,则AE的长为3.
如图,折叠长方形纸片ABCD,先折出对角线BD,再将AD折叠到BD上,得到折痕DE,点A的对应点是点F,若AB=8,BC=6,则AE的长为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{■=8}\\{★=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{■=8}\\{★=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{■=5}\\{★=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{■=3}\\{★=8}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
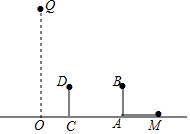 如图,身高1.6米的小明站在距路灯底部O点10米的点A处,他的身高(线段AB)在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.
如图,身高1.6米的小明站在距路灯底部O点10米的点A处,他的身高(线段AB)在路灯下的影子为线段AM,已知路灯灯杆OQ垂直于路面.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com