练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．计算或化简
    （1）计算：|$\sqrt{3}$-2|+20170-（$\frac{1}{3}$）-13tan30°； 
    （2）解方程：x（x+2）=5x+10．

    分析 （1）根据实数的混合运算顺序和法则计算可得；
    （2）因式分解法求解可得．

    解答 解：（1）原式=2-$\sqrt{3}$+1-3×3×$\frac{\sqrt{3}}{3}$
    =3-$\sqrt{3}$-3$\sqrt{3}$
    =3-4$\sqrt{3}$；

    （2）∵x（x+2）-5（x+2）=0，
    ∴（x+2）（x-5）=0，
    则x+2=0或x-5=0，
    解得：x1=-2  x2=5．

    点评 本题主要考查解一元二次方程的能力和实数的混合运算，熟练掌握实数的混合运算顺序和法则和解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

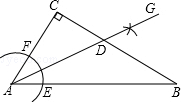    10．如图，在△ABC中，∠C=90°，∠CAB=56°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于$\frac{1}{2}$EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（　　）
    A．34°B．52°C．58°D．62°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．西安市组织长跑队和自行车队宣传全民健身，全程共10千米，两队同时出发，自行车队速度是长跑队速度的2.5倍，结果长跑队比自行车队晚到终点1小时，则自行车队的速度为15千米/时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．将二次函数y=x2的图象向左平移1个单位，则平移后的二次函数的解析式为（　　）
    A．y=x2-1B．y=x2+1C．y=（x-1）2D．y=（x+1）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上．
    （1）随机地抽取一张，求P（奇数）；
    （2）随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，求组成的两位数是4的倍数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

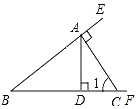    5．如图，已知点A是射线BE上一点，过A作CA⊥BE交射线BF于点C，AD⊥BF交射线BF于点D，给出下列结论：
    ①∠1是∠B的余角；                   ②图中互余的角共有4对；
    ③∠1的补角只有∠ACF；               ④与∠ADB互补的角共有3个．
    其中正确结论有①②④．（把你认为正确的结论的序号都填上）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

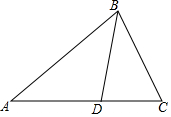    12．已知：如图，在△ABC中，D是AC上一点，$\frac{CB}{CD}$=$\frac{CA}{CB}$=$\frac{3}{2}$，△BCD的周长是24cm．
    （1）求△ABC的周长；
    （2）求△BCD与△ABD的面积比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，说明它是假命题的反例可以是（　　）
    A．∠1=50°，∠2=40°B．∠1=50°，∠2=50°C．∠1=40°，∠2=40°D．∠1=∠2=45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列计算正确的是（　　）
    A．（a+b）2=a2+b2B．（b-a）2=b2-2ab+a2C．（a+2b）（a-2b）=a2-2b2D．（a-b）2=a2-2ab-b2

    查看答案和解析>>

    同步练习册答案