
【题目】某地区在一次九年级数学质量检测试题中,有一道分值为8分的解答题,所有考生的得分只有四种,即:0分,3分,5分,8分,老师为了解本题学生得分情况,从全区4500名考生试卷中随机抽取一部分,分析、整理本题学生得分情况并绘制了如下两幅不完整的统计图:
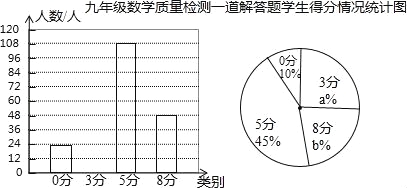
请根据以上信息解答下列问题:
(1)本次调查从全区抽取了 份学生试卷;扇形统计图中a= ,b= ;
(2)补全条形统计图;
(3)该地区这次九年级数学质量检测中,请估计全区考生这道8分解答题的平均得分是多少?得8分的有多少名考生?
【答案】(1)240份,a=25,b=20;(2)补图参见解析;(3)4.6分,900名.
【解析】
试题分析:(1)用得0分24人对应的分率是10%,用除法求得抽取学生试卷数,再求得3分试卷数量,进一步求得3分和8分试卷数量占总数的分率得出a、b的数值即可;(2)利用(1)中的数据补全条形统计图;(3)利用加权平均数的计算方法得出平均得分,利用所占总数的百分数得出得8分的有多少名考生.
试题解析:(1)用得0分24人对应的分率是10%求得抽取学生试卷数,24÷10%=240份,3分试卷数量:240﹣24﹣108﹣48=60份,求a、b的数值:60÷240=25%,48÷240=20%,所以a=25,b=20,故抽取了240份学生试卷,a=25,b=20;(2)如图,根据3分试卷数量是60份补图如下:
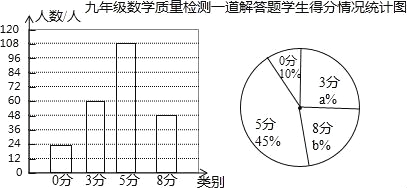
(3)8分解答题的平均得分是:0×10%+3×25%+5×45%+8×20%=4.6分,4500×20%=900名.所以这道8分解答题的平均得分是4.6分;得8分的有900名考生.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如用9枚图钉将4张作品钉在墙上如图).若有28枚图钉可供选用,则最多可以展示绘画作品( )
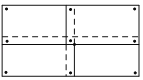
A. 16张B. 18张C. 20张D. 21张
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).
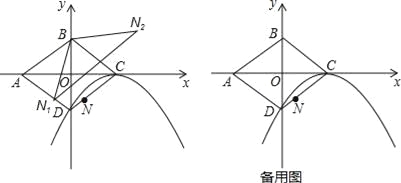
(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A、B两种计算器共100个,要求A种计算器数量不低于B种的![]() ,且不高于B种的
,且不高于B种的![]() .已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.
.已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.
(1)求计划购买这两种计算器所需费用y(元)与x的函数关系式;
(2)问该公司按计划购买者两种计算器有多少种方案?
(3)由于市场行情波动,实际购买时,A种计算器单价下调了3m(m>0)元/个,同时B种计算器单价上调了2m元/个,此时购买这两种计算器所需最少费用为12150元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
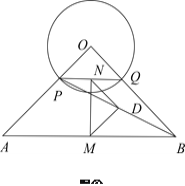
【题目】如图本题图①,在等腰Rt![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,以
上一点,以![]() 为半径作
为半径作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,线段
,线段![]() 、
、![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() 、
、![]() .
.
(1)试探究![]() 是什么特殊三角形?说明理由;
是什么特殊三角形?说明理由;
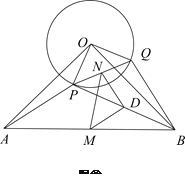
(2)将![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
(3)若![]() ,把
,把![]() 绕点
绕点![]() 在平面内自由旋转,求
在平面内自由旋转,求![]() 的面积y的最大值与最小值的差.
的面积y的最大值与最小值的差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com