
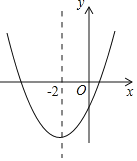
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФДѓжТЭМЯѓШчЭМЫљЪОЃЌЖЅЕузјБъЮЊЃЈЉ2ЃЌЉ9aЃЉЃЌЯТСаНсТлЃКЂй4a+2b+cЃО0ЃЛЂк5aЉb+c=0ЃЛЂлШєЗНГЬaЃЈx+5ЃЉЃЈxЉ1ЃЉ=Љ1гаСНИіИљx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђЉ5ЃМx1ЃМx2ЃМ1ЃЛЂмШєЗНГЬ|ax2+bx+c|=1гаЫФИіИљЃЌдђетЫФИіИљЕФКЭЮЊЉ4ЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ЁОД№АИЁПB
ЁОНтЮіЁПИљОнХзЮяЯпЕФЖЅЕузјБъЃЈЉ2ЃЌЉ9aЃЉЃЌИљОнЖЅЕузјБъЙЋЪНПЩЧѓЕУb=4aЃЌc=-5aЃЌДгЖјПЩЕУХзЮяЯпЕФНтЮіЪНЮЊy=ax2+4axЉ5aЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪвЛвЛХаЖЯМДПЩЃЎ
Ёрa>0ЃЌ
ЁпХзЮяЯпЕФЖЅЕузјБъЃЈЉ2ЃЌЉ9aЃЉЃЌ
ЁрЉ![]() =Љ2ЃЌ
=Љ2ЃЌ![]() =Љ9aЃЌ
=Љ9aЃЌ
Ёрb=4aЃЌc=-5aЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=ax2+4axЉ5aЃЌ
Ёр4a+2b+c=4a+8aЉ5a=7aЃО0ЃЌЙЪЂйе§ШЗЃЌ
5aЉb+c=5aЉ4aЉ5a=Љ4aЃМ0ЃЌЙЪЂкДэЮѓЃЌ
ЁпХзЮяЯпy=ax2+4axЉ5aНЛxжсгкЃЈЉ5ЃЌ0ЃЉЃЌЃЈ1ЃЌ0ЃЉЃЌ
ЁрШєЗНГЬaЃЈx+5ЃЉЃЈxЉ1ЃЉ=Љ1гаСНИіИљx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђЉ5ЃМx1ЃМx2ЃМ1ЃЌе§ШЗЃЌЙЪЂле§ШЗЃЌ
ШєЗНГЬ|ax2+bx+c|=1гаЫФИіИљЃЌдђетЫФИіИљЕФКЭЮЊЉ8ЃЌЙЪЂмДэЮѓЃЌ
ЙЪбЁBЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњУПЬьВЮМгЛЇЭтЛюЖЏЕФЧщПіЃЌЫцЛњГщВщСЫ100УћбЇЩњУПЬьВЮМгЛЇЭтЛюЖЏЕФЪБМфЧщПіЃЌВЂНЋГщВщНсЙћЛцжЦГЩШчЭМЫљЪОЕФЩШаЮЭГМЦЭМЃЎ
ЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЧыжБНгаДГіЭМжа![]() ЕФжЕЃЌВЂЧѓГіБОДЮГщВщжабЇЩњУПЬьВЮМгЛЇЭтЛюЖЏЪБМфЕФжаЮЛЪ§ЃЛ
ЕФжЕЃЌВЂЧѓГіБОДЮГщВщжабЇЩњУПЬьВЮМгЛЇЭтЛюЖЏЪБМфЕФжаЮЛЪ§ЃЛ
ЃЈ2ЃЉЧѓБОДЮГщВщжабЇЩњУПЬьВЮМгЛЇЭтЛюЖЏЕФЦНОљЪБМфЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
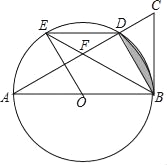
ЁОЬтФПЁПШчЭМЃЌвдЁїABCЕФБпABЮЊжБОЖЛЁбOЃЌНЛACгкЕуDЃЌАыОЖOEЁЮBDЃЌСЌНгBEЃЌDEЃЌBDЃЌЩшBEНЛACгкЕуFЃЌШєЁЯDEBЃНЁЯDBCЃЎ
ЃЈ1ЃЉЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєBFЃНBCЃН2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
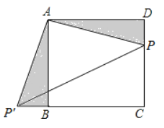
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌЕу
ЪЧе§ЗНаЮЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() КѓФмЙЛгы
КѓФмЙЛгы![]() жиКЯЃЌШє
жиКЯЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЪдЧѓ
ЃЌЪдЧѓ![]() ЕФГЄЪЧ__________ЃЎ
ЕФГЄЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
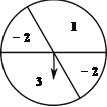
ЁОЬтФПЁПШчЭМЃЌПЩвдздгЩзЊЖЏЕФзЊХЬБЛЫќЕФСНЬѕжБОЖЗжГЩСЫЫФИіЗжБ№БъгаЪ§зжЕФЩШаЮЧјгђЃЌЦфжаБъгаЪ§зжЁА1ЁБЕФЩШаЮдВаФНЧЮЊ120ЁуЃЎзЊЖЏзЊХЬЃЌД§зЊХЬздЖЏЭЃжЙКѓЃЌжИеыжИЯђвЛИіЩШаЮЕФФкВПЃЌдђИУЩШаЮФкЕФЪ§зжМДЮЊзЊГіЕФЪ§зжЃЌДЫЪБЃЌГЦЮЊзЊЖЏзЊХЬвЛДЮЃЈШєжИеыжИЯђСНИіЩШаЮЕФНЛЯпЃЌдђВЛМЦзЊЖЏЕФДЮЪ§ЃЌжиаТзЊЖЏзЊХЬЃЌжБЕНжИеыжИЯђвЛИіЩШаЮЕФФкВПЮЊжЙЃЉ
(1)зЊЖЏзЊХЬвЛДЮЃЌЧѓзЊГіЕФЪ§зжЪЧЃ2ЕФИХТЪЃЛ
(2)зЊЖЏзЊХЬСНДЮЃЌгУЪїзДЭМЛђСаБэЗЈЧѓетСНДЮЗжБ№зЊГіЕФЪ§зжжЎЛ§ЮЊе§Ъ§ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁДЯКЭаЁУїбиЭЌвЛЬѕТЗЭЌЪБДгбЇаЃГіЗЂЕНФГГЌЪаЙКЮяЃЌбЇаЃгыГЌЪаЕФТЗГЬЪЧ4ЧЇУзЃЎаЁДЯЦяздааГЕЃЌаЁУїВНааЃЌЕБаЁДЯДгдТЗЛиЕНбЇаЃЪБЃЌаЁУїИеКУЕНДяГЌЪаЃЎЭМжаелЯпOЉAЉBЉCКЭЯпЖЮODЗжБ№БэЪОСНШЫРыбЇаЃЕФТЗГЬsЃЈЧЇУзЃЉгыЫљОЙ§ЕФЪБМфtЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЌЧыИљОнЭМЯѓЛиД№ЯТСаЮЪЬтЃК
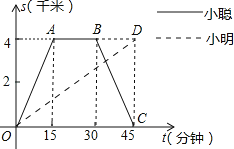
ЃЈ1ЃЉаЁДЯдкГЌЪаЙКЮяЕФЪБМфЮЊЁЁ ЁЁЗжжгЃЌаЁДЯЗЕЛибЇаЃЕФЫйЖШЮЊЁЁ ЁЁ ЧЇУз/ЗжжгЃЛ
ЃЈ2ЃЉЧыФуЧѓГіаЁУїРыПЊбЇаЃЕФТЗГЬsЃЈЧЇУзЃЉгыЫљОЙ§ЕФЪБМфtЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБаЁДЯгыаЁУїгУцЯргіЪБЃЌЫћУЧРыбЇаЃЕФТЗГЬЪЧЖрЩйЧЇУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЎвбжЊAЁЂBСНЕуЕФзјБъЗжБ№ЮЊA(0ЃЌ![]() )ЃЌB(2ЃЌ0)ЃЎжБЯпABгыЗДБШР§КЏЪ§
)ЃЌB(2ЃЌ0)ЃЎжБЯпABгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕуCКЭЕуD(
ЕФЭМЯѓНЛгкЕуCКЭЕуD(![]() 1ЃЌa)ЃЎ
1ЃЌa)ЃЎ
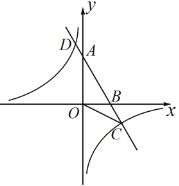
ЃЈ1ЃЉЧѓжБЯпABКЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЧѓЁЯACOЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌКЏЪ§
жаЃЌКЏЪ§![]() ЕФЭМЯѓгыжБЯп
ЕФЭМЯѓгыжБЯп![]() НЛгкЕуA(3,m).
НЛгкЕуA(3,m).
ЃЈ1ЃЉЧѓkЁЂmЕФжЕЃЛ
ЃЈ2ЃЉвбжЊЕуP(nЃЌn)(n>0)ЃЌЙ§ЕуPзїЦНаагк![]() жсЕФжБЯпЃЌНЛжБЯпy=x-2гкЕуMЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпЃЌНЛКЏЪ§
жсЕФжБЯпЃЌНЛжБЯпy=x-2гкЕуMЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпЃЌНЛКЏЪ§![]() ЕФЭМЯѓгкЕуN.
ЕФЭМЯѓгкЕуN.
ЂйЕБn=1ЪБЃЌХаЖЯЯпЖЮPMгыPNЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЂкШєPNЁнPMЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГіnЕФШЁжЕЗЖЮЇ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯвABЃЌCDЪЧЁбOЕФСНЬѕЦНааЯвЃЌЁбOЕФАыОЖЮЊ5ЃЌAB=8ЃЌCD=6ЃЌдђABЃЌCDжЎМфЕФОрРыЮЊЃЈ ЃЉ
A. 7 B. 1 C. 4Лђ3 D. 7Лђ1
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com