
【题目】生活与数学
(1)吉姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么第一个数是 ;

(2)玛丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是 ;
![]()
(3)莉莉也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是 ;

(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号;
(5)若干个偶数按每行8个数排成下图:
①图中方框内的9个数的和与中间的数的关系是 ;

②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是 ;

③托马斯也画了一个斜框,斜框内9个数的和为252,则斜框的中间一个数是 .
【答案】(1)4;(2) 7、8、13、14;(3)10;(4)29;(5)①9个数的和是中间数的9倍;
②40;③28
【解析】
(1)先根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;
(2)先根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;
(3)先根据日历上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;
(4)先根据日历,上的数据规律把所要求的数用代数式表示,用一元一次方程求解即可;
(5)①根据已知9个数直接求出和即可,进而得出与中间的数的关系;
②③根据①中规律得出即可.
(1)设第一个数是x,其他的数为x+ 1,x+ 7,x+8,则x+x+1+x+7+x+8= 32,解得x=4;这四个数是:4,5,11,12;故答案为:4,5,11,12,所以第一个数为4;
(2)设第一个数是x,其他的数为x+ 1,x+6,x+ 7,则x+x+1+x+6+x+ 7= 42,解得x= 7,x+1=8,x+6= 13,x+ 7= 14;故答案为:7,8,13,14;
(3)设中间的数是x,则5x= 50,解得x= 10;故答案为:10;
(4)设最后一个星期日是x,x-7,x-14,x-21,x-28,则x+x-7+x-14+x-21+x-28=75,解得:x=29,故答案为29;
(5)①∵2+4+6+18+20+22+34+36+38=180,180÷20=9,∴方框内的9个数的和是中间的数的9倍,②中间一个数=360÷9=40,故答案为40;③中间一个数=252÷9=28,故答案为28.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,则线段AC扫过的扇形所围成的圆锥体的底面半径是单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
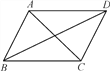
A. 当AB=BC时,它是菱形 B. 当AC=BD时,它是正方形
C. 当∠ABC=90°时,它是矩形 D. 当AC⊥BD时,它是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,灯的质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利润21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表所示:
等级(x级) | 一级 | 二级 | 三级 | … |
生产量(y台/天) | 78 | 76 | 74 | … |
(1)已知护眼灯每天的生产量y(台)是等级x(级)的一次函数,请直接写出y与x之间的函数关系式:;
(2)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 . 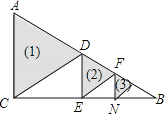
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+![]() a2)+(3b+
a2)+(3b+![]() a2)+…+(9b+
a2)+…+(9b+![]() a2)的值.
a2)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com