
ЁОЬтФПЁПзлКЯгыЪЕМљ
ВйзїЗЂЯжЃК
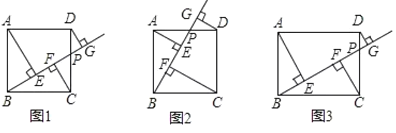
ШчЭМ1КЭЭМ2ЃЌвбжЊЕу![]() ЮЊе§ЗНаЮ
ЮЊе§ЗНаЮ![]() ЕФБп
ЕФБп![]() КЭ
КЭ![]() ЩЯЕФвЛИіЖЏЕуЃЈЕу
ЩЯЕФвЛИіЖЏЕуЃЈЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Г§ЭтЃЉЃЌзїЩфЯп
Г§ЭтЃЉЃЌзїЩфЯп![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дк
дк![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() ЃЌ
ЃЌ![]() Г§ЭтЃЉдЫЖЏЪБЃЌЧѓжЄЃК
Г§ЭтЃЉдЫЖЏЪБЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
 ЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁЁ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕу![]() дк
дк![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() ЃЌ
ЃЌ![]() Г§ЭтЃЉдЫЖЏЪБЃЌЧыжБНгаДГіЯпЖЮ
Г§ЭтЃЉдЫЖЏЪБЃЌЧыжБНгаДГіЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЛ
ЭиЙуЬНЫїЃК
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌевГігы![]() ЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЛ
ЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ4ЃЉШчЭМ3ЃЌШєЕу![]() ЮЊОиаЮ
ЮЊОиаЮ![]() ЕФБп
ЕФБп![]() ЩЯвЛЕуЃЌзїЩфЯп
ЩЯвЛЕуЃЌзїЩфЯп![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЎШє
ЃЎШє![]()
![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() _______ЃЎ
_______ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉ
ЃЛРэгЩМћНтЮіЃЛЃЈ4ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)зїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌЕУЕНЫФБпаЮDGFHЮЊОиаЮЃЌжЄЕУCF+ DG =CHЃЌЩшЗЈжЄЕУ![]() ЃЌЕУЕНAE=CHЃЌМДПЩжЄЕУНсТлЃЛ
ЃЌЕУЕНAE=CHЃЌМДПЩжЄЕУНсТлЃЛ
(2)вРее(1)ЕФЗНЗЈМДПЩЕУЕНCF = AE + DGЃЛ
(3)ИљОн(1)ЕФЗНЗЈжЄЕУ![]() ЃЌЕУЕНAE=BFЃЌBE=CFЃЌРћгУ(1)ЕФНсТлПЩЧѓЕУEF= DGЃЛ
ЃЌЕУЕНAE=BFЃЌBE=CFЃЌРћгУ(1)ЕФНсТлПЩЧѓЕУEF= DGЃЛ
(4)зїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌЕУЕНЫФБпаЮDGFHЮЊОиаЮЃЌЕУЕН DG= CH- CFЃЌИљОнвбжЊЬѕМўвзжЄЕУ![]() ЃЌПЩЧѓЕУ
ЃЌПЩЧѓЕУ![]() ЃЌ
ЃЌ![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌПЩЕУЕН
ЃЌПЩЕУЕН![]() ЃЌЧѓЕУ
ЃЌЧѓЕУ![]() ЃЌМДПЩЧѓЕУНсТлЃЎ
ЃЌМДПЩЧѓЕУНсТлЃЎ
(1)Й§DзїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌШчЭМЃЌ
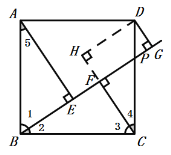
ЁпCFЁЭBGЃЌDGЁЭBGЃЌ
ЁрЫФБпаЮDGFHЮЊОиаЮЃЌ
ЁрDG=HFЃЌ
ЁрCF+ DG= CF+ HF =CHЃЌ
ЁпЫФБпаЮABCDЮЊе§ЗНаЮЃЌЧвAEЁЭBGЃЌ
ЁрAB=CDЃЌЁЯABC=ЁЯBCD=ЁЯAEB=90![]() ЃЌ
ЃЌ
ЁрЁЯ5+ЁЯ1=90![]() ЃЌЁЯ1+ЁЯ2=90
ЃЌЁЯ1+ЁЯ2=90![]() ЃЌЁЯ2+ЁЯ3=90
ЃЌЁЯ2+ЁЯ3=90![]() ЃЌЁЯ3+ЁЯ4=90
ЃЌЁЯ3+ЁЯ4=90![]() ЃЌ
ЃЌ
ЁрЁЯ5=ЁЯ4ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
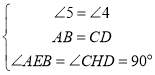 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE=CHЃЌ
ЁрAE= CF+ DGЃЛ
(2)CF = AE + DGЃЛ
вРее(1)ЕФЗНЗЈЃЌШчЭМЃЌМДПЩжЄУїCF = AE + DGЃЛ
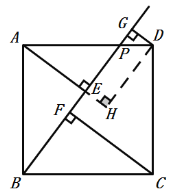
(3)EF= DGЃЌРэгЩШчЯТЃЌШчЭМЃК

гЩ(1)ЕУЃКЁЯ5+ЁЯ1=90![]() ЃЌЁЯ1+ЁЯ2=90
ЃЌЁЯ1+ЁЯ2=90![]() ЃЌ
ЃЌ
ЁрЁЯ5=ЁЯ2ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
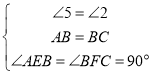 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE=BFЃЌBE=CFЃЌ
ЁрEF=BF-BE=AE-CFЃЌ
ЁпAE= CF+ DGЃЌ
ЁрEF= DGЃЛ
(4)Й§DзїDHЁЮBGНЛCFбгГЄЯпгкЕуHЃЌШчЭМЃЌ
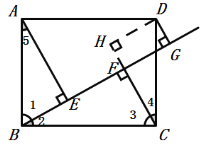
ЁпCFЁЭBGЃЌDGЁЭBGЃЌ
ЁрЫФБпаЮDGFHЮЊОиаЮЃЌ
ЁрDG=HFЃЌ
ЁрDG= CH- CFЃЌ
ЁпЫФБпаЮABCDЮЊОиаЮЃЌAEЁЭBGЃЌCD=2BE=6ЃЌ
ЁрAB=CD=2BE =6ЃЌBE =3ЃЌЁЯABC=ЁЯBCD=ЁЯAEB=90![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯABC=ЁЯBCD=ЁЯAEB=90![]() ЃЌ
ЃЌ
ЁрЁЯ5+ЁЯ1=90![]() ЃЌЁЯ1+ЁЯ2=90
ЃЌЁЯ1+ЁЯ2=90![]() ЃЌЁЯ2+ЁЯ3=90
ЃЌЁЯ2+ЁЯ3=90![]() ЃЌЁЯ3+ЁЯ4=90
ЃЌЁЯ3+ЁЯ4=90![]() ЃЌ
ЃЌ
ЁрЁЯ5=ЁЯ4=ЁЯ2=30![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇЮЊСЫЗсИЛбЇЩњЕФПЮгрЩњЛюЃЌМЦЛЎЙКТђХХЧђКЭРКЧђЙЉЧђРраЫШЄаЁзщЛюЖЏЪЙгУЃЌШєЙКТђ4ИіРКЧђКЭ3ИіХХЧђашгУ94дЊЃЛШєЙКТђ16ИіРКЧђКЭ5ИіХХЧђашгУ306дЊЃЛ
ЃЈ1ЃЉЧѓвЛИіРКЧђКЭвЛИіХХЧђИїЖрЩйдЊЃЛ
ЃЈ2ЃЉИУжабЇОіЖЈЙКТђХХЧђКЭРКЧђЙВ40ИіЃЌзмЗбгУВЛГЌЙ§550дЊЃЌФЧУДИУжабЇжСЩйПЩвдЙКТђЖрЩйИіХХЧђЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
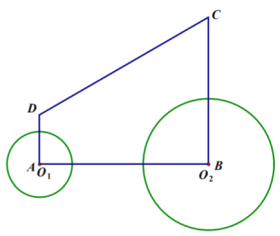
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЕФЖЅЕузјБъЮЊ
ЕФЖЅЕузјБъЮЊ![]() ЃЌЧвгы
ЃЌЧвгы![]() жсНЛгкЕуC
жсНЛгкЕуC![]() ЃЌгы
ЃЌгы![]() жсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФгвВрЃЉЃЎ
жсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФгвВрЃЉЃЎ
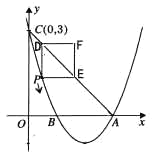
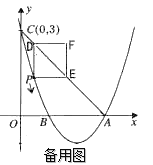
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕуPЪЧИУХзЮяЯпЩЯвЛЖЏЕуЃЌДгЕуCбиХзЮяЯпЯђЕуAдЫЖЏЃЈЕуPгыAВЛжиКЯЃЉЃЌЙ§ЕуPзїPDЁЮ![]() жсЃЌНЛжБЯпACгкЕуDЃЛзїPEЁЮxжсЃЌНЛжБЯпACгкЕуEЃЌвдPDЃЌPEЮЊБпЕФОиаЮPEFDЃЌЮЪОиаЮPEFDжмГЄЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіДЫЪБPЕуЕФзјБъМАзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
жсЃЌНЛжБЯпACгкЕуDЃЛзїPEЁЮxжсЃЌНЛжБЯпACгкЕуEЃЌвдPDЃЌPEЮЊБпЕФОиаЮPEFDЃЌЮЪОиаЮPEFDжмГЄЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіДЫЪБPЕуЕФзјБъМАзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЮЪЬтЃЈ2ЃЉЕФЬѕМўЯТЃЌPЕуТњзуЁЯDAP=90ЁуЃЌЧвЕуEдк![]() жсЩЯЃЌЕуFдкХзЮяЯпЩЯЃЌЮЪЪЧЗёДцдквдAЁЂPЁЂEЁЂFЮЊЖЅЕуЕФЦНааЫФБпаЮЃПШєДцдкЃЌЧѓЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
жсЩЯЃЌЕуFдкХзЮяЯпЩЯЃЌЮЪЪЧЗёДцдквдAЁЂPЁЂEЁЂFЮЊЖЅЕуЕФЦНааЫФБпаЮЃПШєДцдкЃЌЧѓЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁДЯКЭаЁЛлШЅФГЗчОАЧјгЮРРЃЌСНШЫдкОАЕуЙХЩВДІХіУцЃЌЯрдМвЛЦ№ШЅгЮРРОАЕуЗЩЦйЃЌаЁДЯЦяздааГЕЯШааГіЗЂЃЌаЁЛлГЫЕчЖЏГЕГіЗЂЃЌЭООЖВнЕщгЮЭцКѓЃЌдйГЫЕчЖЏГЕШЅЗЩЦйЃЌНсЙћСНШЫЭЌЪБЕНДяЗЩЦй.ЭМжаЯпЖЮ![]() КЭелЯп
КЭелЯп![]() БэЪОаЁДЯЁЂаЁЛлРыЙХЩВЕФТЗГЬ
БэЪОаЁДЯЁЂаЁЛлРыЙХЩВЕФТЗГЬ![]() ЃЈУзЃЉгыаЁДЯЕФЦяааЪБМф
ЃЈУзЃЉгыаЁДЯЕФЦяааЪБМф![]() ЃЈЗжЃЉЕФКЏЪ§ЙиЯЕЕФЭМЯѓЃЌИљОнЭМжаЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈЗжЃЉЕФКЏЪ§ЙиЯЕЕФЭМЯѓЃЌИљОнЭМжаЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
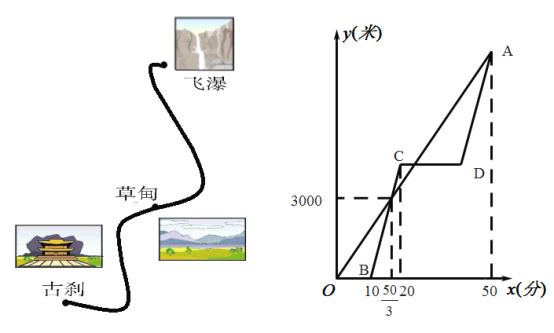
ЃЈ1ЃЉаЁДЯЕФЫйЖШЪЧЖрЩйУз/ЗжЃПДгЙХЩВЕНЗЩЦйЕФТЗГЬЪЧЖрЩйУзЃП
ЃЈ2ЃЉЕБаЁЛлЕквЛДЮгыаЁДЯЯргіЪБЃЌаЁЛлРыВнЕщЛЙгаЖрЩйУзЃП
ЃЈ3ЃЉдкЕчЖЏГЕааЪЛЫйЖШВЛБфЕФЬѕМўЯТЃЌЧѓаЁЛлдкВнЕщгЮЭцЕФЪБМф.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
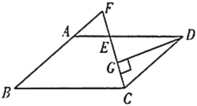
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжмГЄЮЊ_______ЃЎ
ЕФжмГЄЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙтУїжабЇЮЊСЫНтОХФъМЖХЎЭЌбЇЕФЬхг§ПМЪдзМБИЧщПіЃЌЫцЛњГщШЁВПЗжХЎЭЌбЇНјааСЫ800УзХмВтЪдЃЎАДееГЩМЈЗжЮЊгХауЁЂСМКУЁЂКЯИёгыВЛКЯИёЫФИіЕШМЖЃЎбЇаЃЛцжЦСЫШчЯТВЛЭъећЕФЭГМЦЭМЃЎ
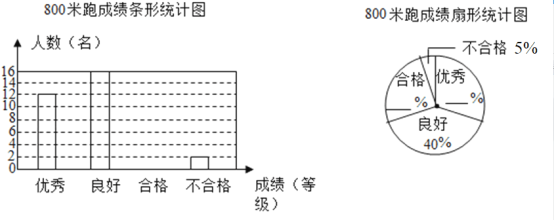
ЃЈ1ЃЉИљОнИјГіЕФаХЯЂЃЌВЙШЋСНЗљЭГМЦЭМЃЛ
ЃЈ2ЃЉИУаЃОХФъМЖга400УћХЎЩњЃЌЧыЙРМЦГЩМЈЮДДяЕНСМКУгаЖрЩйУћЃП
ЃЈ3ЃЉФГАрМзЁЂввСНЮЛГЩМЈгХауЕФЭЌбЇБЛбЁжаВЮМгМДНЋОйааЕФбЇаЃдЫЖЏЛс800УзБШШќЃЎдЄШќЗжБ№ЮЊAЁЂBЁЂCШ§зщНјааЃЌбЁЪжгЩГщЧЉШЗЖЈЗжзщЃЎЧыгУСаБэЛђЪїзДЭМЧѓМзЁЂввСНШЫЧЁКУЗждкЭЌвЛзщЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
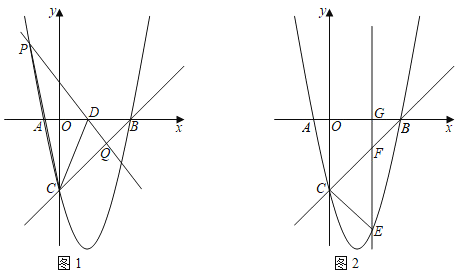
ЁОЬтФПЁПХзЮяЯпyЃНax2+bxЉ5ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЦфжаЕуAзјБъЮЊ(Љ1ЃЌ0)ЃЌвЛДЮКЏЪ§yЃНx+kЕФЭМЯѓОЙ§ЕуBЁЂCЃЎ
ЃЈ1ЃЉЪдЧѓЖўДЮКЏЪ§МАвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуD(2ЃЌ0)ЮЊxжсЩЯвЛЕуЃЌPЮЊХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуPЁЂDзїжБЯпPDНЛЯпЖЮCBгкЕуQЃЌСЌНгPCЁЂDCЃЌШєSЁїCPDЃН3SЁїCQDЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуEЮЊХзЮяЯпЮЛгкжБЯпBCЯТЗНЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуEзїжБЯпEGЁЭxжсгкЕуGЃЌНЛжБЯпBCгкЕуFЃЌЕБEF+![]() CFЕФжЕзюДѓЪБЃЌЧѓЕуEЕФзјБъЃЎ
CFЕФжЕзюДѓЪБЃЌЧѓЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧвЦфжавЛИіИљЮЊСэвЛИіИљЕФвЛАыЃЌдђГЦетбљЕФЗНГЬЮЊЁААыЕШЗжИљЗНГЬЁБЃЎ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧвЦфжавЛИіИљЮЊСэвЛИіИљЕФвЛАыЃЌдђГЦетбљЕФЗНГЬЮЊЁААыЕШЗжИљЗНГЬЁБЃЎ
ЃЈ1ЃЉЂйЗНГЬ![]() АыЕШЗжИљЗНГЬЃЈЬюЁАЪЧЁБЛђЁАВЛЪЧЁБЃЉЃЛ
АыЕШЗжИљЗНГЬЃЈЬюЁАЪЧЁБЛђЁАВЛЪЧЁБЃЉЃЛ
ЂкШє![]() ЪЧАыЕШЗжИљЗНГЬЃЌдђДњЪ§ЪН
ЪЧАыЕШЗжИљЗНГЬЃЌдђДњЪ§ЪН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌдђЙигк
ЕФЭМЯѓЩЯЃЌдђЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЪЧАыЕШЗжИљЗНГЬТ№ЃПВЂЫЕУїРэгЩЃЛ
ЪЧАыЕШЗжИљЗНГЬТ№ЃПВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЙћЗНГЬ![]() ЪЧАыЕШЗжИљЗНГЬЃЌЧвЯрвьСНЕу
ЪЧАыЕШЗжИљЗНГЬЃЌЧвЯрвьСНЕу![]() ЃЌ
ЃЌ![]() ЖМдкХзЮяЯп
ЖМдкХзЮяЯп![]() ЩЯЃЌЪдЫЕУїЗНГЬ
ЩЯЃЌЪдЫЕУїЗНГЬ![]() ЕФвЛИіИљЮЊ
ЕФвЛИіИљЮЊ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБНЧЬнаЮ![]() жаЃЌ
жаЃЌ![]() ЕФдВаФ
ЕФдВаФ![]() ДгЕу
ДгЕу![]() ПЊЪМбиелЯп
ПЊЪМбиелЯп![]() вд
вд![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дЫЖЏЃЌ
дЫЖЏЃЌ![]() ЕФдВаФ
ЕФдВаФ![]() ДгЕу
ДгЕу![]() ПЊЪМби
ПЊЪМби![]() Бпвд
Бпвд![]()
![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дЫЖЏЃЌ
дЫЖЏЃЌ![]() АыОЖЮЊ
АыОЖЮЊ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌШє
ЃЌШє![]() ЗжБ№ДгЕу
ЗжБ№ДгЕу![]() ЁЂЕу
ЁЂЕу![]() ЭЌЪБГіЗЂЃЌдЫЖЏЕФЪБМфЮЊ
ЭЌЪБГіЗЂЃЌдЫЖЏЕФЪБМфЮЊ![]()
ЃЈ1ЃЉЧыЧѓГі![]() гыбќ
гыбќ![]() ЯрЧаЪБ
ЯрЧаЪБ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉдк![]() ЗЖЮЇФкЃЌЕБ
ЗЖЮЇФкЃЌЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() гы
гы![]() ЭтЧаЃП
ЭтЧаЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com