
 ��1����֪m�Ƿ���x2-x-1=0��һ��������m��m+1��2-m2��m+3��+4��ֵ��
��1����֪m�Ƿ���x2-x-1=0��һ��������m��m+1��2-m2��m+3��+4��ֵ������ ��1����m�Ƿ���x2-x-1=0��һ��������x=m���뷽�̵õ�����m�ĵ�ʽ�����κ��������ʽ�ӵ�ֵ��
��2������y=2x+2����y=0�����B�����꣬Ȼ�����A�����꣬���ô���ϵ������÷����������Ľ���ʽ��
�ڸ���ƽ���ߵ����ʼ���ֱ�����D�����꣬Ȼ����뷴���������Ľ���ʽ�жϼ��ɣ�
��� �⣺��1����m�Ƿ���x2-x-1=0��һ������
��m2-m=1��
��m��m+1��2-m2��m+3��+4=-m2+m+4=-��m2-m-4��=3��
��2������y=2x+2����y=0����x=-1��
��B�������ǣ�-1��0����
��A��ֱ��y=2x+2�ϣ�
��A�������ǣ�1��4����
��A��1��4���ڷ���������y=$\frac{k}{x}$ͼ����
��k=4��
�෴���������Ľ���ʽΪ��y=$\frac{4}{x}$��
�ڡ��ı���ABCD��ƽ���ı��Σ�
��D�������ǣ�2��2������0��6������-2��-6����
��D��2��2���ڷ���������y=$\frac{4}{x}$��ͼ���ϣ�
���� ���⿼����һԪ���η��̵ĸ������̵Ľ�Ķ��壬����ϵ����������������ʽ���ô���ϵ����ȷ�������Ľ���ʽ���dz��õ�һ�ֽ��ⷽ����ͬѧ��Ҫ�����������ַ�����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ������������ֽƬABC������AB=AC���ѡ�B��EM�۵���ʹ��B���ڵ�D�ϣ��ѡ�C��FN�۵���ʹ��CҲ���ڵ�D�ϣ�
��ͼ��ʾ��һ������������ֽƬABC������AB=AC���ѡ�B��EM�۵���ʹ��B���ڵ�D�ϣ��ѡ�C��FN�۵���ʹ��CҲ���ڵ�D�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ABCD������AEF���ڽ��ڡ�O��EF��BC��CD�ֱ��ཻ�ڵ�G��H����$\frac{EF}{GH}$��ֵ�ǣ�������
��ͼ��������ABCD������AEF���ڽ��ڡ�O��EF��BC��CD�ֱ��ཻ�ڵ�G��H����$\frac{EF}{GH}$��ֵ�ǣ�������| A�� | $\frac{\sqrt{6}}{2}$ | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ABCD�У�AB=4��AD=5��AD��AB��BC�ֱ����O������E��F��G���㣬����D����O������BC�ڵ�M���е�ΪN����DM�ij�Ϊ��������
��ͼ���ھ���ABCD�У�AB=4��AD=5��AD��AB��BC�ֱ����O������E��F��G���㣬����D����O������BC�ڵ�M���е�ΪN����DM�ij�Ϊ��������| A�� | $\frac{13}{3}$ | B�� | $\frac{9}{2}$ | C�� | $\frac{4}{3}$$\sqrt{13}$ | D�� | 2$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������y=-x2+bx+c��x�ύ�ڵ�A��m-2��0����B��2m+1��0������A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪP���Գ���Ϊl��x=1��
��֪������y=-x2+bx+c��x�ύ�ڵ�A��m-2��0����B��2m+1��0������A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪP���Գ���Ϊl��x=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -16x-0.5 | B�� | -16x+0.5 | C�� | 16x-8 | D�� | -16x+8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������35 | B�� | ��λ����34 | C�� | ƽ������35 | D�� | ������6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
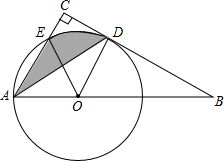 ��ͼ����OΪRt��ABCб��AB��һ�㣬��OAΪ�뾶�ġ�O��BC���ڵ�D����AC���ڵ�E������AD��
��ͼ����OΪRt��ABCб��AB��һ�㣬��OAΪ�뾶�ġ�O��BC���ڵ�D����AC���ڵ�E������AD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com