
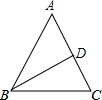
 如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是85°.
如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是85°.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
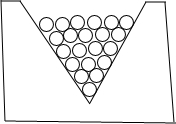 如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.
如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.| 最上层的产品数(支) | 1 | 2 | 3 | 4 | … | 10 | … |
| 产品总数 | 1 | 3 | 6 | 10 | … | 55 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
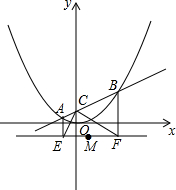 阅读理解
阅读理解查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 33 | B. | 32 | C. | 31 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 方差 | D. | 众数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com